
【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;

(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.

【答案】(1)①证明见试题解析;②![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)①根据旋转的性质和平行线的性质证明;
②过A作AF⊥BC于F,过C作CE⊥AB于E,根据等腰三角形的性质和三角形的面积公式解答;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,和以C为圆心BC为半径画圆交BC的延长线于F1,得出最大和最小值解答即可.
试题解析:(1)①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图1:
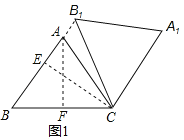
∵AB=AC,AF⊥BC,BC=6,
∴BF=CF=3,
∴B1C=BC=6,
可得:B1B=2BE,
∵EC=![]() ,
,
∴BE=![]() ,则BB1=
,则BB1=![]() ,
,
故AB1=![]() ﹣5=
﹣5=![]() ,
,
∴△AB1C的面积为:![]() ;
;
(2)如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,
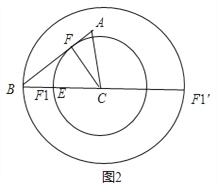
此时在Rt△BFC中,CF=![]() ,
,
∴CF1=![]() ,
,
∴EF1的最小值为![]() ﹣3=
﹣3=![]() ;
;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为9﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,
(1)∠AED和∠ABC可看成是直线__________、__________被直线__________所截得的__________角;
(2)∠EDB和∠DBC可看成是直线__________、__________被直线__________所截得的__________角;
(3)∠EDC和∠C可看成是直线__________、__________被直线__________所截得的__________角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某楼盘准备以每平方10 000元的均价对外销售由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方8 100元的均价开盘销售,则平均每次下调的百分率是( )
A.8%B.9%C.10%D.11%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) 
A.AB=BE
B.BE⊥DC
C.∠ADB=90°
D.CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①对顶角相等;
②等角的补角相等;
③两直线平行,同旁内角相等;
④在同一平面内,过一点有且只有一条直线与已知直线垂直
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com