
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .过点
.过点![]() 且与直线
且与直线![]() 平行的直线交
平行的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
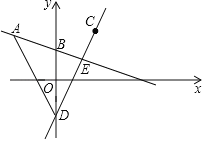
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)10.
;(2)10.
【解析】
(1)先求得A的坐标,即可求得C的坐标,根据题意设直线CD的解析式为y![]() x+b,代入C的坐标,根据待定系数法求得即可;
x+b,代入C的坐标,根据待定系数法求得即可;
(2)根据图象坐标特征求得B、D的坐标,然后解析式联立求得E的坐标,根据S△ADE=S△ABD+S△EBD即可求得.
(1)∵直线y![]() x+2过点A(﹣3,m),
x+2过点A(﹣3,m),
∴m![]() (﹣3)+2=3,
(﹣3)+2=3,
∴A(﹣3,3).
∵点A关于y轴的对称点为点C,
∴C(3,3).
∵直线CD与直线y![]() x平行,
x平行,
∴设直线CD的解析式为y![]() x+b,
x+b,
代入C(3,3)得:3![]() 3+b,
3+b,
解得:b=﹣2,
∴直线CD的解析式为![]() ;
;
(2)在直线y![]() x+2中,令x=0,则y=2,
x+2中,令x=0,则y=2,
∴B(0,2),
在直线y![]() x﹣2中,令x=0,则y=﹣2,
x﹣2中,令x=0,则y=﹣2,
∴D(0,﹣2),
∴BD=4,
解 ,得
,得![]() ,
,
∴E(2,![]() ),
),
∴S△ADE=S△ABD+S△EBD![]() 10.
10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一条笔直的公路上有
,一条笔直的公路上有![]() 、
、![]() 、
、![]() 三地
三地![]() 、
、![]() 两地相距
两地相距![]() 千米,甲、乙两个野外徒步爱好小组从
千米,甲、乙两个野外徒步爱好小组从 ![]() 、
、![]() 两地同时出发,沿公路始终匀速相向而行,分别走向
两地同时出发,沿公路始终匀速相向而行,分别走向![]() 、
、![]() 两地.甲、乙两组到
两地.甲、乙两组到![]() 地的距离
地的距离![]() ,
,![]() (千米)与行走时间
(千米)与行走时间![]() (时)的关系如图
(时)的关系如图![]() 所示.
所示.
(1)请在图![]() 中标出
中标出![]() 地的位置,并写出相应的距离:
地的位置,并写出相应的距离:![]()
![]() ;
;
(2)在图![]() 中求出甲组到达
中求出甲组到达![]() 地的时间
地的时间![]() ;
;
(3)求岀乙组从![]() 地到
地到![]() 地行走过程中
地行走过程中![]() 与行走时间
与行走时间![]() 的关系式.
的关系式.
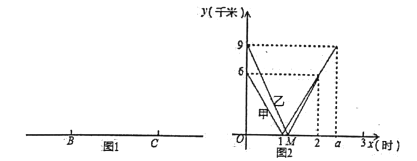
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在11月中旬对甲、乙、丙三种型号的电视机进行促销.其中,甲型号电视机直接按成本价1280元的基础上获利![]() 定价;乙型号电视机在原销售价2199元的基础上先让利199元,再按八五折优惠;丙型号电视机直接在原销售价2399元上减499元;活动结束后,三种型号电视机总销售额为20600元,若在此次促销活动中,甲、乙、丙三种型号的电视机至少卖出其中两种型号,则三种型号的电视机共______有种销售方案.
定价;乙型号电视机在原销售价2199元的基础上先让利199元,再按八五折优惠;丙型号电视机直接在原销售价2399元上减499元;活动结束后,三种型号电视机总销售额为20600元,若在此次促销活动中,甲、乙、丙三种型号的电视机至少卖出其中两种型号,则三种型号的电视机共______有种销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() (a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣
(a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣![]() ),该抛物线与BE交于另一点F,连接BC.
),该抛物线与BE交于另一点F,连接BC.
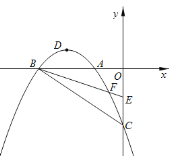
(1)求该抛物线的解析式,并用配方法把解析式化为![]() 的形式;
的形式;
(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=![]() (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为![]() ,则k的值为_____.
,则k的值为_____.
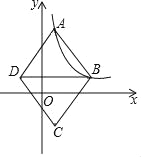
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市教育行政部门为了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)请你根据图中的信息,回答下列问题:
(1)该校初二学生总人数为____________,扇形统计图中的![]() 的值为____________,扇形统计图中“活动时间为4天”的扇形所对圆心角度数为______________;
的值为____________,扇形统计图中“活动时间为4天”的扇形所对圆心角度数为______________;
(2)请把条形统计图补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 方向向点
方向向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,
运动,![]() 同时出发,当点
同时出发,当点![]() 停止运动时,点
停止运动时,点![]() 也随之停止,设点
也随之停止,设点![]() 运动的时间为
运动的时间为![]() 秒.请回答下列问题:
秒.请回答下列问题:
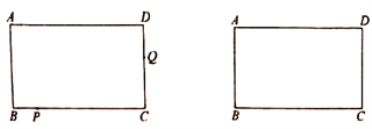
(1)请用含![]() 的式子表达
的式子表达![]() 的面积
的面积![]() ,并直接写出
,并直接写出![]() 的取值范围.
的取值范围.
(2)是否存在某个![]() 值,使得
值,使得![]() 和
和![]() 全等?若存在,请求出所有满足条件的
全等?若存在,请求出所有满足条件的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com