
分析 (1)直接利用立方差公式分解因式得出答案;
(2)直接利用十字相乘法分解因式再结合平方差公式分解因式得出答案;
(3)把第一、二、五项组合在一起运用完全平方公式,第三、四项组合在一起提公因式,然后再运用提公因式法分解即可;
(4)首先把前三项利用式子相乘法分解,然后把后边的三项写成4(x+2y)-(3x-y)-4的形式,然后利用提公因式法即可分解.
解答 解:(1)a3+1=(a+1)(a2-a+1);
(2)4x4-13x2+9
=(x2-1)(4x2-9)
=(x+1)(x-1)(2x+3)(2x-3);
(3)b2+c2+2ab+2ac+2bc
=b2+2bc+c2+2ab+2ac
=(b+c)2+2a(b+c)
=(b+c)(b+c+2a);
(4)3x2+5xy-2y2+x+9y-4
=(x+2y)(3x-y)+x+9y-4
=(x+2y)(3x-y)+(4x+8y-3x+y)-4
=(x+2y)(3x-y)+4(x+2y)-(3x-y)-4
=(x+2y)(3x-y)-(3x-y)+4(x+2y)-4
=(x+2y-1)(3x-y)+4(x+2y-1)
=(x+2y-1)(3x-y+4).
点评 本题考查了分组分解法分解因式,分解时要注意认真观察各项之间的联系,根据提公因式法、平方差公式或完全平方公式进行组合是解题的关键.


科目:初中数学 来源: 题型:解答题
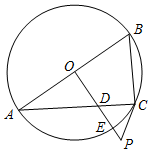 如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,线段AB=20cm,点P沿线段AB自A点向B点以2cm/秒运动,同时点Q沿线段BA自B点向A点以3cm/秒运动,4秒后P、Q两点相遇.
如图,线段AB=20cm,点P沿线段AB自A点向B点以2cm/秒运动,同时点Q沿线段BA自B点向A点以3cm/秒运动,4秒后P、Q两点相遇.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com