
2
|
| ||
| 4 |
| ||
| 4 |
| 1 | ||||
|
| 3 |
| 2 |
| 3 |
| 2 |
| ||||
|
|
| 8 |
| 5 |
| 8 |
| 5 |
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:阅读理解
| 2 |
| 3 |
| 9 |
| 12 |
| a |
| a•b |
| a |
| b |
|
| ||
|
|
| ||
| 3 |
| 27 |
| 3 |
| 2 |
| 75 |
| 18 |
|
|
| 3 |
| 2 |
| 75 |
| 18 |
|
|
| 3 |
查看答案和解析>>
科目:初中数学 来源:走向清华北大·初二数学 题型:044
将下列各式化成最简二次根式:
①x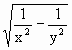 ;
;
②2a![]() (a>b);
(a>b);
③![]() (a>1);
(a>1);
④![]() (0<a<2,b>0);
(0<a<2,b>0);
⑤![]() (x>y);
(x>y);
⑥![]() (b>a>0);
(b>a>0);
⑦![]() ;
;
⑧![]() ;
;
⑨![]() ;
;
⑩![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读下列短文,回答有关问题:
在实数这章中,遇到过 、
、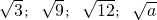 ;这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开的尽方,可以利用
;这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开的尽方,可以利用 将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时,这样的二次根式叫做最简二次根式,
将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时,这样的二次根式叫做最简二次根式,
例如,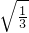 化成最简二次根式是
化成最简二次根式是 ,
, 化成最简二次根式是
化成最简二次根式是 .几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子就是同类二次根式.
.几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子就是同类二次根式.
(1)请判断下列各式中,哪些是同类二次根式?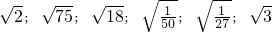 ;
;
(2)二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算: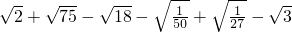 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com