
(2014•涉县一模)如图,AD为⊙O直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:对于甲乙两人的作法,可判断( )
甲:①以D为圆心,OD长为半径作圆弧,交⊙O于B.C两点.
②连接AB,BC,CA.△ABC即为所求的三角形
乙:①作OD的中垂线,交⊙O于B,C两点.
②连接AB,BC.△ABC即为所求三角形.
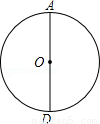
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
C
【解析】
试题分析:甲的作法.连接DB、DC,由作图可知,DB=DO=DC,在⊙O中可知OB=OD=OC,故可得出△OBD和△OCD都是等边三角形,再根据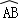 =
=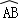 ,
,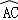 =
=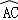 可知∠ODB=∠ACB=60°,∠ABC=∠ODC=60°,故可得出结论;
可知∠ODB=∠ACB=60°,∠ABC=∠ODC=60°,故可得出结论;
乙的作法,连接OB、OC.根据AD为⊙O的直径,BC是半径OD的垂直平分线,由垂径定理可知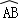 =
=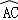 ,
, =
=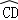 ,OE=
,OE= OD=
OD= OC,所以AB=AC.在Rt△OEC中由锐角三角函数的定义可得出cos∠EOC的值,进而可求出∠EOC的度数,进而可得出结论.
OC,所以AB=AC.在Rt△OEC中由锐角三角函数的定义可得出cos∠EOC的值,进而可求出∠EOC的度数,进而可得出结论.
【解析】
甲的作法.如图2;
证明:连接DB、DC.
由作图可知:
DB=DO=DC,
在⊙O中,
∴OB=OD=OC,
∴△OBD和△OCD都是等边三角形,
∴∠ODB=∠ODC=60°,
∵ =
= ,
,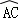 =
=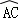 ,
,
∴∠ODB=∠ACB=60°,∠ABC=∠ODC=60°,
∴△ABC是等边三角形.
乙的作法如图1,
证明:连接OB、OC.
∵AD为⊙O的直径,BC是半径OD的垂直平分线,
∴ =
=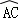 ,
,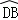 =
= ,OE=
,OE= OD=
OD= OC,
OC,
∴AB=AC.
在Rt△OEC中,
∴cos∠EOC= =
= ,
,
∴∠EOC=60°,
∴∠BOC=120°.
∴∠BAC=60°.
∴△ABC是等边三角形.
故选:C.




 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:2014-2015学年广东省广州市番禺区九年级上学期期末模拟质量抽测数学试卷(解析版) 题型:选择题
如图,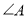 是⊙O的圆周角,
是⊙O的圆周角, ,则
,则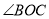 的度数为( ).
的度数为( ).
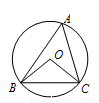
(A)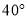 (B)
(B)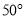 (C)
(C)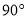 (D)
(D)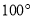
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 14.2勾股定理的应用练习卷(解析版) 题型:?????
(2014•石家庄二模)如图,若圆柱的底面周长是30cm,高是40cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是( )
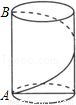
A.80cm B.70cm C.60cm D.50cm
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.5逆命题与逆定理练习卷(解析版) 题型:?????
用反证法证明“三角形的三个外角中至少有两个钝角”时,假设正确的是( )
A.假设三个外角都是锐角 B.假设至少有一个钝角
C.假设三个外角都是钝角 D.假设三个外角中只有一个钝角
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.5逆命题与逆定理练习卷(解析版) 题型:?????
(2013•江东区模拟)要说明命题:“一组对边平行且对角线相等的四边形是矩形”是假命题,可以举的反例是( )
A.等腰梯形 B.矩形 C.菱形 D.直角梯形
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.4尺规作图练习卷(解析版) 题型:?????
(2014•将乐县质检)如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( )

A.以点C为圆心,OD为半径的弧
B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DM为半径的弧
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.4尺规作图练习卷(解析版) 题型:?????
(2014•葫芦岛)观察图中尺规作图痕迹,下列结论错误的是( )

A.PQ为∠APB的平分线
B.PA=PB
C.点A、B到PQ的距离不相等
D.∠APQ=∠BPQ
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.1命题、定理与证明练习卷(解析版) 题型:?????
(2014•襄阳)下列命题错误的是( )
A.所有的实数都可用数轴上的点表示
B.等角的补角相等
C.无理数包括正无理数,0,负无理数
D.两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 12.3乘法公式练习卷(解析版) 题型:?????
(2014•莆田)下列运算正确的是( )
A.a3•a2=a6 B.(2a)3=6a3 C.(a﹣b)2=a2﹣b2 D.3a2﹣a2=2a2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com