
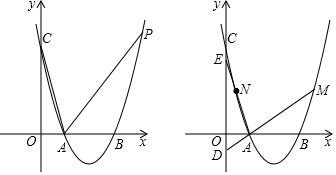
分析 (1)把A点坐标代入y=mx2-4mx+3中求出m的值即可得到抛物线的解析式;
(2)先确定C(0,3),则利用勾股定理计算出AC=$\sqrt{10}$,取AC的中点Q,作OH⊥AC于H,PK⊥x轴于K,如图1,设P(x,x2-4x+3),利用直角三角形斜边上的中线性质、勾股定理和面积法求出OQ=$\frac{\sqrt{10}}{2}$,OH=$\frac{3\sqrt{10}}{10}$,HQ=$\frac{2\sqrt{10}}{5}$,再证明△PAK∽△OQH,然后利用相似比得到关于x的方程,再解方程求出x即可得到P点坐标;
(3)设M(t,t2-4t+3),利用对称性得到N(4-t,t2-4t+3),再利用待定系数法分别求出直线AM的解析式为y=(t-3)x+3-t和直线AN的解析式为y=(1-t)x+t-1,从而得到D点和E点坐标,然后可计算出OE-OD的值.
解答 解:(1)把A(1,0)代入y=mx2-4mx+3得m-4m+3=0,解得m=1,
所以抛物线的解析式为y=x2-4x+3;
(2)当x=0时,y=x2-4x+3=3,则C(0,3),
AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
取AC的中点Q,作OH⊥AC于H,PK⊥x轴于K,如图1,设P(x,x2-4x+3),
∴OQ=$\frac{1}{2}$AC=$\frac{\sqrt{10}}{2}$,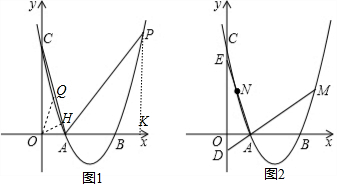
∵$\frac{1}{2}$OH•AC=$\frac{1}{2}$•OA•OC,
∴OH=$\frac{1×3}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$,
∴HQ=$\sqrt{O{Q}^{2}-O{H}^{2}}$=$\frac{2\sqrt{10}}{5}$,
∵CQ为斜边AC上的中线,
∴QC=QO,
∴∠QCO=∠QOC,
∴∠OQH=∠QCO+∠QOC=2∠QCO,
∵∠PAB=2∠ACO,
∴∠OQH=∠PAB,
∴△PAK∽△OQH,
∴PK:OH=AK:QH,即(x2-4x+3):$\frac{3\sqrt{10}}{10}$=(x-1):$\frac{2\sqrt{10}}{5}$,
整理得4x2-19x+15=0,解得x1=1,x2=$\frac{15}{4}$,
∴P($\frac{15}{4}$,$\frac{33}{16}$);
(3)设M(t,t2-4t+3),
∵M与N两点关于抛物线的对称轴对称,
∴N(4-t,t2-4t+3),
设直线AM的解析式为y=kx+b,
把A(1,0),M(t,t2-4t+3)代入得$\left\{\begin{array}{l}{k+b=0}\\{kt+b={t}^{2}-4t+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=t-3}\\{b=3-t}\end{array}\right.$,
∴直线AM的解析式为y=(t-3)x+3-t,
∴D(0,3-t),
同样可得直线AN的解析式为y=(1-t)x+t-1,
∴E(0,t-1),
∴OE-OD=t-1-(t-3)=2.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和直角三角形斜边上的中线性质;会利用待定系数法求函数解析式;会利用勾股定理和相似比计算线段的长;理解坐标与图形的性质.在(2)中构建△PAK∽△OQH是解决问题的关键.


科目:初中数学 来源: 题型:解答题
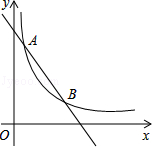 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:
某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{11}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com