Question

已知等腰三角形一腰上的高与另一腰的夹角等于50°，设这条高与等腰三角形底边上的高所在的直线的夹角中，有一个锐角为α，则α的度数为________．

Answer 1

70°或20°
分析：根据题意画出图象，根据等腰三角形性质求出∠C=∠ABC，根据∠BEC=90°求出∠C，求出∠EBC，根据三角形内角和定理求出即可．
解答：分为两种情况：①如图1，
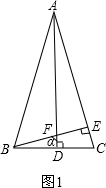
∵AB=AC，
∴∠C=∠ABC，
∵∠ABE=50°，
∴∠EBC=∠C-50°，
∵BE⊥AC，
∴∠BEC=90°，
∴∠C+∠EBC=90°，
∴∠C-50°+∠C=90°，
∴∠C=70°，
∴∠EBC=70°-50°=20°，
∵AD⊥BC，
∴∠ADB=90°，
∴α=∠BFD=90°-∠EBC=90°-20°=70°；
②如图2，
∵AB=AC，
∴∠C=∠ABC，
∵∠ABE=50°，
∴∠EBC=∠C+50°，
∵BE⊥AC，
∴∠BEC=90°，
∴∠C+∠EBC=90°，
∴∠C+50°+∠C=90°，
∴∠C=20°，
∴∠EBC=20°+50°=70°，
∵AD⊥BC，
∴∠ADB=90°，
∴α=∠BFD=90°-∠EBC=90°-70°=20°；
故答案为：70°或20°．
点评：本题考查了等腰三角形性质，三角形内角和定理的应用，关键是求出∠C和∠EBC的度数．