
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
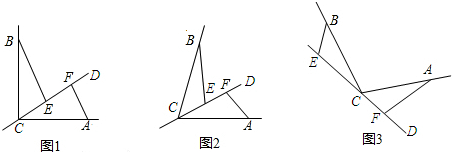
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC和点S在平面直角坐标系中的位置如图所示.
△ABC和点S在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
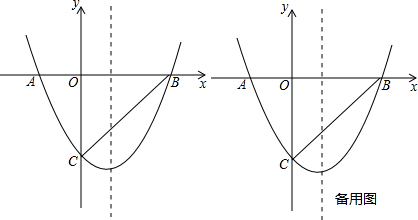
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明同学参加周末社会实践活动,到“富平花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:
小明同学参加周末社会实践活动,到“富平花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:| 个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
| 频数 | 2 | 5 | 7 | 4 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com