
分析 (1)根据题意可以列出相应的方程,从而可以求得相应的售价;
(2)根据题意可以得到利润与售价之间的函数关系式,然后化为顶点式,即可解答本题.
解答 解:(1)要使平均每天的销售利润为1200元,设售价为x元/只,
(x-40)[90-(x-50)×3]=1200,
解得,x1=x2=60,
即要使平均每天的销售利润为1200元,售价为60元/只;
(2)设每只售价为x元,利润为W元,
W=(x-40)[90-(x-50)×3]=-3(x-60)2+1200,
∵x≤55,
∴当x=55时,W取得最大值,此时W=1125,
即每只玩具的售价为55元时,可获得最大利润,最大利润是1125元.
点评 本题考查二次函数的应用、一元二次方程的应用,解答此类问题的关键是明确题意,列出相应的函数解析式和方程,根据二次函数的顶点式和自变量的取值范围求出函数的最值.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 161,18 | B. | 162,17 | C. | 162,18 | D. | 161,17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
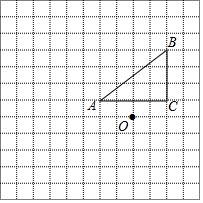 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′查看答案和解析>>
科目:初中数学 来源: 题型:填空题
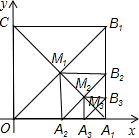 如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以A1M1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以A1M2为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标是($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1;以A1M1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以A1M2为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;…依此类推,这样作的第n个正方形对角线交点Mn的坐标是($\frac{{2}^{n}-1}{{2}^{n}}$,$\frac{1}{{2}^{n}}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$或$-\frac{5}{4}$ | B. | $\frac{3}{4}$或$\frac{5}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com