
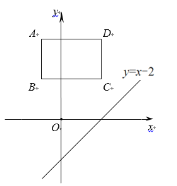
【题目】如图,四边形ABCD是矩形,AD∥![]() 轴,点B的坐标为 (-1,2),点D的坐标为(2,4),将直线y=x-2向上平移m个单位,使平移后的直线恰好经过点D .
轴,点B的坐标为 (-1,2),点D的坐标为(2,4),将直线y=x-2向上平移m个单位,使平移后的直线恰好经过点D .
(1)求m的值;
(2)平移后的直线与矩形的边BC交于点E,求△CDE的面积.
【答案】(1)4;(2)1.
【解析】
(1)根据直线平移的规律,可设平移后的直线解析式为y=x+b,把点A(2,4)代入,求出b=2,得到平移后的直线解析式为y=x+2,进而求出m=2-(-2)=4;
(2)先求出点E的纵坐标为2,再把y=2代入y=x+2,那么点E的坐标为(0,2),CE=2,根据三角形面积公式即可求出△ABE的面积.
(1)设平移后的直线解析式为y=x+b,
∵y=x+b过点A(2,4),
∴4=2+b,
∴b=2,
∴平移后的直线解析式为y=x+2,
∴m=2-(-2)=4;
(2)如图,
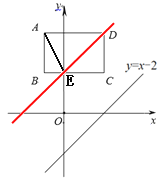
∵矩形ABCD中,AD∥y轴,点B的坐标为(-1,2),
∴点E的纵坐标为2.
把y=2代入y=x+2,得x=0,
∴点E的坐标为(0,2),
∴BE=1,
∴△ABE的面积=![]() ×2×1=1.
×2×1=1.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问:
(1)用含t的代数式表示动点P在运动过程中距O点的距离;
(2)P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?
(3)是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A. x2-6=(10-x)2B. x2-62=(10-x)2
C. x2+62=(10-x)2D. x2+6=(10-x)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)为积极响应政府提出的“绿色发展低碳出行”号召,某自行车厂决定生产一批共享单车投入市场.该厂原计划一周生产1400辆共享单车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

⑴根据记录可知前三天共生产 辆;
⑵产量最多的一天比产量最少的一天多生产 辆;
⑶该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简
(1)-18+21+(-13)
(2)-81÷![]() ×
×![]() ÷(-16)
÷(-16)
(3)(![]() +
+![]() -
-![]() )×(-24)
)×(-24)
(4)-22-![]() ×[4-(-3)2]
×[4-(-3)2]
(5)化简:5(3x2y-xy2)-4(-xy2+2x2y)
(6)先化简,再求值:-![]() x+2(x-
x+2(x-![]() y2) - (-
y2) - (-![]() x+
x+![]() y2);其中x=2,y=
y2);其中x=2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
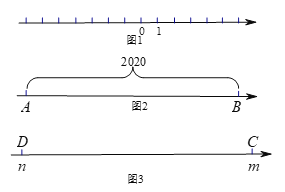
【题目】已知在透明纸面上有一数轴(如图1),折叠透明纸面.
(1)若表示1的点与表示-1的点重合,则表示-7的点与表示 的点重合;
(2)若表示-2的点与表示6的点重合,回答以下问题:
①表示12的点与表示 的点重合;
②如图2,若数轴上AB两点之间的距离为2020(点A在点B的左侧),且AB两点经折叠后重合,则AB两点表示的数分别是 .
(3)如图3,若m和n表示的点C和点D经折叠后重合(m>n),折痕与数轴的交点为折痕点.已知线段CD上两点P、Q (点P在点Q的左侧,PQ<CD),PQ=a.当线段PQ的端点与折痕点重合时,求PQ两点表示的数分别是多少?(用含m,n,a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,反比例函数![]() 的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
(1)直接写出A、B、D三点的坐标;
(2)若将矩形只向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,求反比例函数的解析式和此时直线AC的解析式y=mx+n.并直接写出满足![]() 的x取值范围.
的x取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
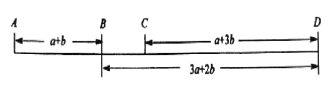
【题目】己知![]() 四个车站的位置如图所示.
四个车站的位置如图所示.
(1)求![]() 两站之间的距离;(用含
两站之间的距离;(用含![]() 的代数式表示)
的代数式表示)
(2)一辆汽车从![]() 站出发,每小时行驶60千米,经过
站出发,每小时行驶60千米,经过![]() 站到达C站(在
站到达C站(在![]() 站没有停留).所用时间为1.5小时.汽车在
站没有停留).所用时间为1.5小时.汽车在![]() 站短暂停留后,继续以相同速度行驶,再行驶2小时到达
站短暂停留后,继续以相同速度行驶,再行驶2小时到达![]() 站,求
站,求![]() 的值以及汽车从
的值以及汽车从![]() 站行驶到
站行驶到![]() 站一共用了多少小时?
站一共用了多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com