
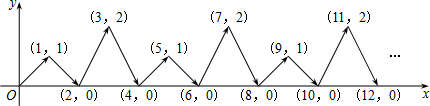
分析 观察可知这些点分为三类:①横坐标为偶数的点,纵坐标为0,②横坐标为4n+1的点的纵坐标为1(n≥0),③横坐标为4n+3的点的纵坐标为2(n≥0),由此不难找到答案.
解答 解:这些点分为三类:①横坐标为偶数的点,纵坐标为0,
②横坐标为4n+1的点的纵坐标为1(n≥0),
③横坐标为4n+3的点的纵坐标为2(n≥0),
∵2017=4×504+1,
∴经过第2017次运动后的点属于第二类,
∴经过第2017次运动后,动点P的坐标(2017,1),
故答案为(2017,1).
点评 本题考查点与坐标的关系,解题的关键是要发现这些点的坐标有什么规律,本题发现这些点的坐标分为三类,是解决问题的突破口.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
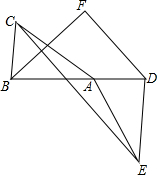 两个全等的△ABC和△EDA如图放置(∠ABC=∠EDA<90°,BC=DA),点B、A、D在同一条直线上,作∠ABC的平分线BF,过点D作DF⊥BF于点F,连接CE,则BF⊥CE,BF=$\frac{1}{2}$CE成立吗?请说明理由.
两个全等的△ABC和△EDA如图放置(∠ABC=∠EDA<90°,BC=DA),点B、A、D在同一条直线上,作∠ABC的平分线BF,过点D作DF⊥BF于点F,连接CE,则BF⊥CE,BF=$\frac{1}{2}$CE成立吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 型号 | 每台售价(万元) | 每台每日污水处理量(吨) |
| A型 | 18 | 160 |
| B型 | 12 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
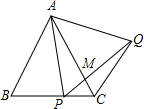 如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )| A. | ①② | B. | ①③ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
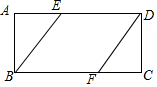 如图,矩形ABCD中,AD=2AB,点E、F分别在AD、BC上,若四边形BFDE为菱形,则AE:ED的值为( )
如图,矩形ABCD中,AD=2AB,点E、F分别在AD、BC上,若四边形BFDE为菱形,则AE:ED的值为( )| A. | 1:2 | B. | 3:5 | C. | $\sqrt{2}$:3 | D. | 3:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com