
 如图,在平面直角坐标系中,?ABCD的一边BC在x轴上,OC=2,点D的坐标为(-3,3),BC=4.
如图,在平面直角坐标系中,?ABCD的一边BC在x轴上,OC=2,点D的坐标为(-3,3),BC=4.分析 (1)根据平行四边形的性质可得出AD=BC=4,结合点D的坐标即可得出点A的坐标;
(2)连接AC、BD交于点E,由OC、BC的长度可得出点B的坐标,结合点D的坐标即可得出点E的坐标,由平行四边形的性质可得出该直线必过点E,再根据点的坐标利用待定系数法求出直线解析式即可.
解答 解:(1)∵四边形ABCD为平行四边形,
∴AD=BC=4.
∵点D的坐标为(-3,3),BC在x轴上,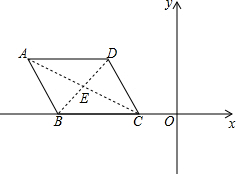
∴点A的坐标为(-7,3).
(2)连接AC、BD交于点E,如图所示.
∵OC=2,BC=4,
∴点B的坐标为(-6,0).
∵点D的坐标为(-3,3),
∴点E的坐标为(-$\frac{9}{2}$,$\frac{3}{2}$).
∵过点(0,2)的直线将?ABCD分割成周长相等的两部分,
∴该直线过点E.
设这条直线的函数解析式为y=kx+b,
将(0,2)、(-$\frac{9}{2}$,$\frac{3}{2}$)代入y=kx+b,
$\left\{\begin{array}{l}{b=2}\\{-\frac{9}{2}k+b=\frac{3}{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{9}}\\{b=2}\end{array}\right.$,
∴这条直线的函数解析式为y=$\frac{1}{9}$x+2.
点评 本题考查了待定系数法求一次函数解析式以及平行四边形的性质,解题的关键是:(1)由点D的坐标利用平行四边形的性质找出点A的坐标;(2)根据平行四边形的性质找出该直线必过平行四边形对角线的交点.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
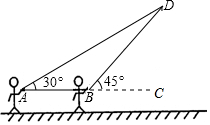 放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)
放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
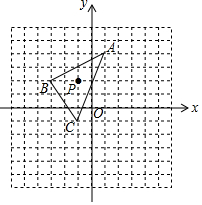 如图,△ABC中任意一点P(m,n),经过平移后对应点P1(m+4,n-3),将△ABC作同样的平移得到△A1B1C1,已知A(1,4)、B(-3,2),C(-1,-1).
如图,△ABC中任意一点P(m,n),经过平移后对应点P1(m+4,n-3),将△ABC作同样的平移得到△A1B1C1,已知A(1,4)、B(-3,2),C(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
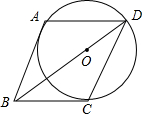 如图,菱形ABCD的顶点A,D,C均在⊙O上,且BC边与⊙O相切于点C.
如图,菱形ABCD的顶点A,D,C均在⊙O上,且BC边与⊙O相切于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
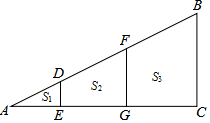 如图,△ABC中,D,F是边AB上两点,DE∥FG∥BC,DF=FB,△ADE的面积为S1,四边形DFGE和四边形FBCG的面积分别为S2,S3.
如图,△ABC中,D,F是边AB上两点,DE∥FG∥BC,DF=FB,△ADE的面积为S1,四边形DFGE和四边形FBCG的面积分别为S2,S3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com