Question

（11·孝感）（满分14分）如图（1），矩形ABCD的一边BC在直接坐标系中x轴上，折叠边AD，使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为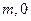（），其中.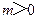
（1）求点E、F的坐标（用含的式子表示）；（5分）
（2）连接OA，若△OAF是等腰三角形，求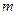的值；（4分）
（3）如图（2），设抛物线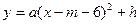经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求、、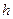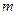的值.（5分）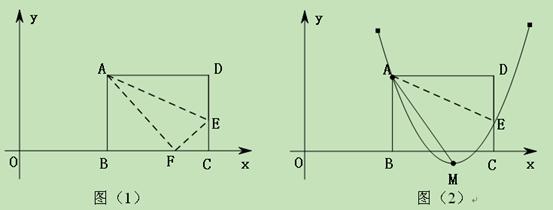

Answer 1

（1）∵四边形ABCD是矩形
∴AD＝BC＝10，AB＝DC＝8，∠D＝∠DCB＝∠ABC＝90°
由折叠对称性：AF＝AD＝10，FE＝DE
∴FC＝4……………………………………2分
设EF＝x，则EC＝8－x
在Rt△ECF中，4²＋(8－x)²＝x² 解得x＝5
∴CE＝8－x＝5
∵B (m，0)  ∴E (m＋10，3)，F (m＋6，0)……………………………………5分
（2）分三种情形讨论：
若AO＝AF，∵AB⊥OF ∴OB＝BF＝6，∴m＝6…………………………………7分
若OF＝AF，则m＋6＝10 解得m＝4
若AO＝OF，在Rt△AOB中，AO²＝OB²＋AB²＝m²＋64  

说明：求对一个m值得2分，求对二个m值得3分，求对三个m值得4分
（3）由（1）知A (m，8)，E (m＋10，3)，
∴M (m＋6，－1)
设对称轴交AD于G

∴G (m＋6，8) ∴AG＝6，GM＝8―(―1)＝9
∵∠OAB＋∠BAM＝90°，∠BAM＋∠MAG＝90°，
∴∠OAB＝∠MAG
又∠ABO＝∠MGA＝90°，
∴△AOB∽△AMG
∴m＝12…………………………………14分

解析