
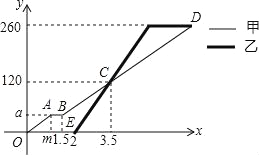
����Ŀ���ס�����̨�������Լӹ���ͬ���������������ʱ����Ч�ʲ��䣬�����ȿ�ʼ��������;ͣ��������0.5Сʱ����ͼ�Ǽס�����̨�������������������и��Լӹ����������y���������������ʱ��x��ʱ��֮��ĺ���ͼ��
��1����ͼ��m��a��ֵ��
��2������������ӹ����������y��x֮��ĺ�����ϵʽ��
��3�����һ��������ڼ䣬����̨�����ӹ�������������50��ʱx��ֵ��
���𰸡�(1) m=1��a=40��(2) y=40x-20��3.5��x��7����(3) ����������![]() Сʱ��
Сʱ��![]() Сʱʱ��ǡ�����50����
Сʱʱ��ǡ�����50����
��������
�������: ��1��������֪��ͼ����Եõ�m��ֵ���ɼס�����̨�������Լӹ���ͬ���������������ʱ����Ч�ʲ��䣬�������a��ֵ��
��2����ͼ����Եõ���B��C�ĵ�����꣬�Ӷ����Եõ��������ӹ����������y��x֮��ĺ�����ϵʽ��
��3��������������г���Ӧ�ĵ�ʽ���Ӷ��������x��ֵ��
�����������1��������ɵã�
m=1.5-0.5=1��
�߹���Ч�ʱ��ֲ��䣬
��![]() �����a=40��
�����a=40��
��m=1��a=40��
��2����������ӹ����������y��x֮��ĺ�����ϵʽ�ǣ�y=k1x+b1��
��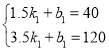 ��
��
��ã�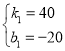
���������ӹ����������y��x֮��ĺ�����ϵʽ�ǣ�y=40x-20��3.5��x��7����
��3����CE����ֱ�ߵĺ�������ʽΪ��y=k2x+b2��
��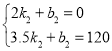
��ã�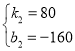 ��
��
��ֱ��CE����ֱ�ߵĽ���ʽΪ��y=80x-160��
��|��80x-160��-��40x-20��|=50��
��ã�x=![]() ��x=
��x=![]() ��
��
������������![]() Сʱ��
Сʱ��![]() Сʱʱ��ǡ�����50����
Сʱʱ��ǡ�����50����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε������߳��ֱ�Ϊ3��7���������ܳ�Ϊ������ ��
A.10
B.13
C.17
D.13��17
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
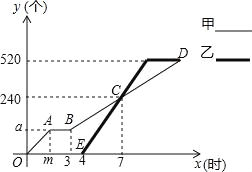
����Ŀ���ס������˸��Լӹ���ͬ��������������ȿ�ʼ��������;���ͣ������1Сʱ�����¹���ʱ���ɰ���ԭ���Ĺ���Ч�ʼӹ��������ͼ�Ǽס������������������и��Լӹ����������y�����������ʱ��x��ʱ��֮��ĺ���ͼ��
��1��ͼ��m= ��a= ��
��2�������¹�����ӹ����������y��x֮��ĺ�����ϵʽ��
��3�����ҹ����ڼ����˼ӹ�������������100��ʱx��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���̵꽫ij�ַ�װ���ɱ������20%���ۣ�����9���Ż����������ÿ����װ�Կɻ���8Ԫ�������ַ�װÿ���ijɱ��ǣ�������
A. 100Ԫ B. 105Ԫ C. 110Ԫ D. 115Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ˮ������Խ��Խ��ľ���ѡ�����þ�ˮ����һ�̳�ץס�̻����ӳ��ҹ�����A��B�����ͺż��þ�ˮ����160̨��A�ͺż��þ�ˮ��������150Ԫ/̨��B�ͺż��þ�ˮ��������350Ԫ/̨�����������ͺŵļ��þ�ˮ������ȥ36000Ԫ��
��1����A��B�����ͺż��þ�ˮ���������˶���̨��
��2��Ϊʹÿ̨B�ͺż��þ�ˮ����ë������A�ͺŵ�2�����ұ�֤������160̨���þ�ˮ����ë������11000Ԫ����ÿ̨A�ͺż��þ�ˮ�����ۼ������Ƕ���Ԫ����ע��ë����=�ۼ۩����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε�һ�߳�Ϊ3 cm���ܳ�Ϊ19 cm����������ε�����Ϊ �� ��
A. 3 cmB. 8 cmC. 3 cm��8 cmD. ���ϴ𰸾�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ��ʾ�����н����У�
��4ac-b2��0����3b+2c��0����4a+c��2b����m��am+b��+b��a��m��-1����
������ȷ�Ľ����У� ��
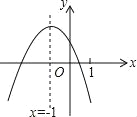
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ε����߳�Ϊ4��5�������ߵij��Ƿ���x2��5x+6=0��һ����������������ε��ܳ��ǣ�������
A. 11 B. 12 C. 11��12 D. 15
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com