
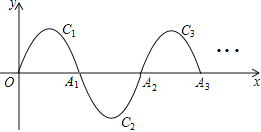
【题目】如图,一段抛物线![]() ,记为抛物线
,记为抛物线![]() ,它与
,它与![]() 轴交于点
轴交于点![]() ;将抛物线
;将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() 得抛物线
得抛物线![]() ,交
,交![]() 轴于点
轴于点![]() ;将抛物线
;将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() 得抛物线
得抛物线![]() ,交
,交![]() 轴于点
轴于点![]() .···如此进行下去,得到一条“波浪线”,若点
.···如此进行下去,得到一条“波浪线”,若点![]() 在此“波浪线”上,则
在此“波浪线”上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
查看答案和解析>>
科目:初中数学 来源: 题型:
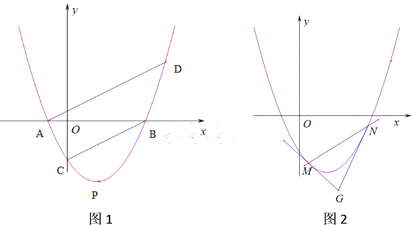
【题目】已知抛物线![]() 与
与![]() 轴交于A,B两点(A在B左边),与
轴交于A,B两点(A在B左边),与![]() 轴交于C点,顶点为P,OC=2AO.
轴交于C点,顶点为P,OC=2AO.
(1)求![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)直线AD//BC,与抛物线交于另一点D,△ADP的面积为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,过(1,-1)的直线与抛物线交于M、N两点,分别过M、N且与抛物线仅有一个公共点的两条直线交于点G,求OG长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两个不透明的盒子,
两个不透明的盒子,![]() 盒中装有红色、黄色、蓝色卡片各1张,
盒中装有红色、黄色、蓝色卡片各1张,![]() 盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从
盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从![]() 、
、![]() 两个盒子中任意摸出一张卡片.
两个盒子中任意摸出一张卡片.
(1)从![]() 盒中摸出红色卡片的概率为______;
盒中摸出红色卡片的概率为______;
(2)用画树状图或列表的方法,求摸出的两张卡片中至少有一张红色卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.

(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于![]() MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
A.15°B.45°C.15°或30°D.15°或45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 汕头国际马拉松赛事设有“马拉松(
汕头国际马拉松赛事设有“马拉松(![]() 公里)”,“半程马拉松(
公里)”,“半程马拉松(![]() 公里)”,“迷你马拉松(
公里)”,“迷你马拉松(![]() 公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小红被分配到“马拉松(![]() 公里)”项目组的概率为___________.
公里)”项目组的概率为___________.
(2)用树状图或列表法求小红和小青被分到同一个项目组进行志愿服务的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com