
 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).分析 (1)利用勾股定理得出BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=20,AB=$\sqrt{C{D}^{2}+(AD-BC)^{2}}$=13;
(2)以B,P,Q为顶点的三角形为等腰三角形有三种情况:当PB=PQ时,当PQ=BQ时,当BP=BQ时,由等腰三角形的性质就可以得出结论;
(3)点P、Q关于BD对称,也就是BP=BQ,由(2)的计算直接判定即可.
解答 解:(1)BD=20,AB=13;
(2)如图,
过P作PM⊥BC于M,由图可知:CM=PD=2t,CQ=t,
若以B,P,Q三点为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,
由PQ2=BQ2,得t2+122=(16-t)2,解得t=$\frac{7}{2}$;
②若PB=PQ,由PB2=PQ2,得(16-2t)2+122=t2+122,
整理,得3t2-64t+256=0,
解得,t=$\frac{16}{3}$,t2=16(不合题意,舍去),
③若BP=BQ,在Rt△PMB中,BP2=(16-2t)2+122,
由BP2=BQ2,得(16-2t)2+122=(16-t)2,即3t2-32t+144=0,
∵△=-704<0,
∴3t2-32t+144=0无解,
∴BP≠BQ;
综合上面的讨论可知:当t=$\frac{7}{2}$或$\frac{16}{3}$时,
以B,P,Q三点为顶点的三角形是等腰三角形;
(3)不存在点P、Q关于BD对称.
理由∵P、Q关于BD对称,
∴BD垂直平分PQ,
则BP=BQ,
在Rt△PMB中,BP2=(16-2t)2+122,
由BP2=BQ2,得(16-2t)2+122=(16-t)2,即3t2-32t+144=0,
∵△=-704<0,
∴3t2-32t+144=0无解,
∴BP≠BQ,
∴不存在点P、Q关于BD对称.
点评 此题考查四边形的综合题,有关梯形的问题可以通过作高线可以转化为直角三角形与矩形的问题.并且要理解以B、P、Q三点为顶点的三角形是等腰三角形,应分①若PQ=BQ,②若BP=BQ,③若PB=PQ.三种情况进行讨论.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 实数a,b在轴上的位置如图所示,化简:$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$.
实数a,b在轴上的位置如图所示,化简:$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
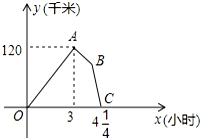 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,则快递车从乙地返回时的速度为90千米/时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com