
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).

(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+2时x的取值范围.
【答案】(1)y=x2-2x-3(2)x<-1或x>4
【解析】试题分析:(1)、首先根据一次函数的解析式分别求出点A和点B的坐标,然后利用待定系数法求出二次函数的解析式;(2)、根据描点法在坐标系中画出函数图像,需要注意两个函数的交点坐标;(3)、根据函数的交点将x轴分别三部分,然后根据每部分图像的位置关系得出函数值的大小关系.
试题解析:(1)∵二次函数y=x2+bx+c的图象与与直线y=x+1相交于点A(-1,m)和点B(n,5),∴m=-1+1=0,n+1=5,即n=4,∴点A(-1,0)和点B(4,5),∴![]() ,解得
,解得![]() ,即二次函数的解析式为y=x2-2x-3;
,即二次函数的解析式为y=x2-2x-3;
(2)这两个函数图象的草图如图所示:
 ,
,
x的取值范围为x<-1或x>4


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
【题目】统计数据显示,2018年6月中国出口钢材694.4万吨,同比增长2%,1﹣6月中国出口钢材3542.6万吨,同比减少13.2%,其中数据“694.4万”用科学记数法表示为( )
A. 694.4×104 B. 6.944×105 C. 69.44×105 D. 6.944×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称 | 空调 | 彩电 | 冰箱 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高最高产值是多少?(以千元为单位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点坐标为E(1,0),与
的顶点坐标为E(1,0),与![]() 轴的交点坐标为(0,1).
轴的交点坐标为(0,1).
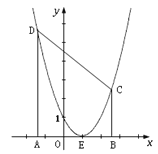

(1)求该抛物线的函数关系式.
(2)A、B是![]() 轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥
轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥![]() 轴交抛物线于D,
轴交抛物线于D,
过B作BC⊥![]() 轴交抛物线于C. 设A点的坐标为(
轴交抛物线于C. 设A点的坐标为(![]() ,0),四边形ABCD的面积为S.
,0),四边形ABCD的面积为S.
① 求S与![]() 之间的函数关系式.
之间的函数关系式.
② 求四边形ABCD的最小面积,此时四边形ABCD是什么四边形?
③ 当四边形ABCD面积最小时,在对角线BD上是否存在这样的点P,使得△PAE的周长最小,若存在,请求出点P的坐标及这时△PAE的周长;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B, BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=![]() ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
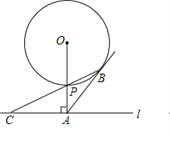

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com