
 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍. .
. x-3.(1分)
x-3.(1分) x-3与y轴交于点C,可知C(0,-3).
x-3与y轴交于点C,可知C(0,-3). 经过点A(4,0)和点C,
经过点A(4,0)和点C,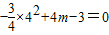 ,
, .
. .(2分)
.(2分) ,
, ,
,
 ,
, ,
, ;(3分)
;(3分)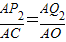 ,
,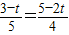
 ;(4分)
;(4分) 或
或 时,△PQA是直角三角形.
时,△PQA是直角三角形.
 DF•AE,S△CDF=
DF•AE,S△CDF= DF•OE.
DF•OE. DF•AE+
DF•AE+ DF•OE
DF•OE DF×(AE+OE)
DF×(AE+OE) ×(DE+EF)×4
×(DE+EF)×4 ×(
×( )×4
)×4 .(6分)
.(6分) (0<x<4).
(0<x<4). ,
, .
. ).(7分)
).(7分)

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2010年北京市朝阳区中考数学一模试卷(解析版) 题型:解答题
 的图象的一个交点为A(2,m),试确定平移后的直线解析式和反比例函数解析式.
的图象的一个交点为A(2,m),试确定平移后的直线解析式和反比例函数解析式.查看答案和解析>>
科目:初中数学 来源:2010年北京市朝阳区中考数学一模试卷(解析版) 题型:解答题
 ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.?
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.?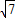 ,问题得到解决.
,问题得到解决. ,BP=
,BP=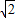 ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.?
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.?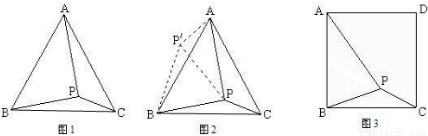
查看答案和解析>>
科目:初中数学 来源:2010年北京市朝阳区中考数学一模试卷(解析版) 题型:解答题
 )
)
查看答案和解析>>
科目:初中数学 来源:2010年北京市朝阳区中考数学一模试卷(解析版) 题型:解答题
| 分数段 | 频数 | 频率 |
| 80≤x<85 | x | 0.2 |
| 85≤x<90 | 80 | y |
| 90≤x<95 | 60 | 0.3 |
| 95≤x<100 | 20 | 0.1 |
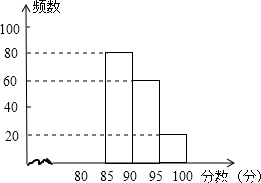
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com