
分析 方程的一个根是x=$\sqrt{4-2\sqrt{3}}$,代入方程,由a,b是整数,列出关于a,b的方程组,解方程组即可求出a、b的值,进而即可求出代数式的值.
解答 解:把x=$\sqrt{4-2\sqrt{3}}$代入方程有:
($\sqrt{4-2\sqrt{3}}$)2+a($\sqrt{3-2\sqrt{3}+1}$)+b=0,
4-2$\sqrt{3}$+($\sqrt{3}$-1)a+b=(a-2)$\sqrt{3}$+4-a+b=0.
∵a,b是整数,
∴$\left\{\begin{array}{l}{a-2=0}\\{4-a+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=-2}\end{array}\right.$,
∴$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{{2}^{2}+(-2)^{2}}{2×(-2)}$=-2.
故答案为:-2.
点评 本题考查的是一元二次方程的解,把方程的解代入方程,根据二次根式的性质化简,得到关于a,b的方程组,求出a,b的值,即可求解.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
 如图,CD分别交AD,EG于点D,G,EB分别交AD,EG于点A,E,AC交EG于点F,FH交AD于点H,AD平分∠BAC,EG∥AD,CG⊥EG,∠C=∠AFH.
如图,CD分别交AD,EG于点D,G,EB分别交AD,EG于点A,E,AC交EG于点F,FH交AD于点H,AD平分∠BAC,EG∥AD,CG⊥EG,∠C=∠AFH.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5.
已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
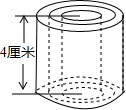 如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com