
分析 根据实数的运算顺序,首先计算乘方、开方和乘法,然后从左向右依次计算,求出算式$\sqrt{27}+{(-\frac{1}{2})^{-1}}-2tan60°-{(-1)^{2016}}$的值是多少即可.
解答 解:$\sqrt{27}+{(-\frac{1}{2})^{-1}}-2tan60°-{(-1)^{2016}}$
=3$\sqrt{3}$-2-2$\sqrt{3}$-1
=$\sqrt{3}$-3
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了特殊角的三角函数值,要牢记30°、45°、60°角的各种三角函数值.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
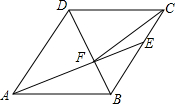 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为12$\sqrt{3}$,其中一定成立的是①②③(把所有正确结论的序号都填在横线上)①②③.
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为12$\sqrt{3}$,其中一定成立的是①②③(把所有正确结论的序号都填在横线上)①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
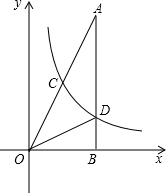 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4,则点C的坐标为(2,4).
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4,则点C的坐标为(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com