
某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头.一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将物品送到军舰.已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
|
解 如图,设两船在E点相遇.
因为 AB⊥BC, AB=BC=200, 所以 AC= ∠C= 过点D作DF⊥BC,垂足为F,则 DF=CF, 即 DF=CF= 设在E点相遇时补给船航行了x海里,即DE=x,那么 AB+BE=2x, EF=AB+BC-(AB+BE)-CF=300-2x. 在Rt△DEF中,根据勾股定理可得方程 x2=1002+(300-2x)2, 整理得 3x2-1200x+100000=0, 解得 x1=200- x2=200+ 所以,相遇时补给船大约航行了118.4海里. 分析 解决本题时,一定要联系有关的几何知识,先作出简易的方位图,再根据题意,画出相应的几何图形,借助有关的几何知识,便不难解决了. |


科目:初中数学 来源: 题型:
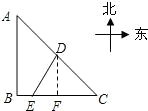 么相遇时补给船航行了多少海里?(结果精确到0.1海里,
么相遇时补给船航行了多少海里?(结果精确到0.1海里,| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
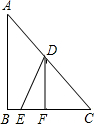 出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
1.小岛D和小岛F相距多少海里?
2.已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)

查看答案和解析>>
科目:初中数学 来源:2011年湖南省长沙市九年级上学期期中模拟考试数学卷 题型:解答题
如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
【小题1】小岛D和小岛F相距多少海里?
【小题2】已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)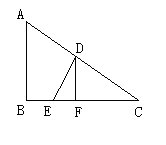
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com