
����Ŀ�������Ķ�����IJ��ϣ�����й����⣺
���ϣ���ѧϰ����ֵʱ���������˽����ֵ�ļ������壬��|5-3|��ʾ5��3�������϶�Ӧ������֮��ľ��룻����|5+3|=|5-��-3��|������|5+3|��ʾ5��-3�������϶�Ӧ������֮��ľ��롣��ˣ�һ��أ���A,B�������Ϸֱ��ʾ������a,b����ôA,B֮��ľ��루Ҳ�����߶�AB�ij��ȣ��ɱ�ʾΪ|a-b|��
������ǿ����þ���ֵ�ļ������尴���·�����![]() ����Сֵ��
����Сֵ��
![]() ��������x��1��Ӧ�ĵ�֮��ľ��룬
��������x��1��Ӧ�ĵ�֮��ľ��룬![]() ��������x��2��Ӧ�ĵ�֮��ľ��룬��������������ͬһ�������ϱ�ʾ������Ȼ��Ѿ�����Ӽ��ɵ�ԭʽ��ֵ.
��������x��2��Ӧ�ĵ�֮��ľ��룬��������������ͬһ�������ϱ�ʾ������Ȼ��Ѿ�����Ӽ��ɵ�ԭʽ��ֵ.
��A��B��P�����Ӧ�����ֱ���1��2��x.
��1��x��2ʱ����P�����߶�AB�ϣ���ʱ![]() ��
��
��x��2ʱ����P����B���Ҳ࣬��ʱ![]() �� PA��PB��AB��2PB��AB��
�� PA��PB��AB��2PB��AB��
��x ��1ʱ����P����A����࣬��ʱ![]() ��PA��PB��AB��2PA��AB��
��PA��PB��AB��2PA��AB��
���Ͽ�֪����1��x��2ʱ��P�����߶�AB�ϣ���![]() ȡ����СֵΪ1��
ȡ����СֵΪ1��
![]()
![]()
![]()
�����������˼�����������������������⣺
��1������![]() ��x��ȡֵ��Χ�� ��
��x��ȡֵ��Χ�� ��
��2����![]() ����СֵΪ �����ֵΪ ��
����СֵΪ �����ֵΪ ��
����ͼ��
![]()
![]()
���𰸡���1��x<-3��x��4����2��-3��3.
��������
��1����������ɷ�����������ۣ���x<-3ʱ����-3��x��4ʱ����x��4ʱ���ֱ����ֵ������ȡֵ��Χ����7���Ƚϼ��ɵó������
��2���ֵ�x��-1ʱ����-1��x��2����x��2ʱ����������ۣ���ȡֵ��Χ�����������ֵ����Сֵ.
�⣺��1����![]() ���������ϱ�ʾ-3��4���㣬
���������ϱ�ʾ-3��4���㣬
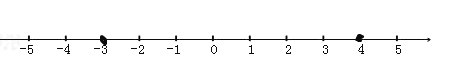
��x<-3ʱ��![]() >7;
>7;
��-3��x��4ʱ��![]() .
.
��x��4ʱ��![]() .
.
�ʵ�x<-3��x��4ʱ![]() .
.
��2��![]()
��x��-1��![]()
��-1��x��2��![]() ����ʱ��x=2ʱ��ȡ�����ֵ3����x=-1ʱ��ȡ����Сֵ-3��
����ʱ��x=2ʱ��ȡ�����ֵ3����x=-1ʱ��ȡ����Сֵ-3��
��x��2ʱ��![]() .
.
��![]() ����СֵΪ-3�����ֵΪ3.
����СֵΪ-3�����ֵΪ3.


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������ij�ֲ�Ʒ��������Ϊ10�����Σ���1���Σ���͵��Σ��IJ�Ʒһ��������95����ÿ������6Ԫ��ÿ���һ�����Σ�ÿ����������2Ԫ����һ���������5����
��1����������![]() ���εIJ�Ʒһ���������Ϊ
���εIJ�Ʒһ���������Ϊ![]() Ԫ������
Ԫ������![]() Ϊ����������1��
����������1��![]() ��10�������
��10�������![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����������x���εIJ�Ʒһ���������Ϊ1120Ԫ����ò�Ʒ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
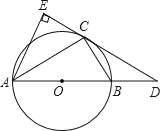
����Ŀ����ͼ����֪��O����ABC�����Բ��AB����O��ֱ����D��AB�ӳ�����һ�㣬AE��DC��DC���ӳ����ڵ�E����ACƽ����EAB��
��1����֤��DE����O�����ߣ�
��2����AB=6��AE=![]() ����BD��BC�ij���
����BD��BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���AD��BE���ڵ�H���ҡ�1=��2=22.5�������н��ۣ��١�1=��3����BD+DH=AB����2AH=BH������CD=![]() ����BH=3������DF��BE�ڵ�F����AE-FH=DF����ȷ����( )��.
����BH=3������DF��BE�ڵ�F����AE-FH=DF����ȷ����( )��.

A. 5B. 4C. 3D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��b�������ϵ�λ����ͼ��ʾ����|a|��|b|�����и�ʽ����ȷ�ĸ����ǣ�������
��a+b��0����b��a��0����![]() ����3a��b��0������a��b��0��
����3a��b��0������a��b��0��
![]()
A. 2��B. 3��C. 4��D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������C����O �ϣ���P��ֱ��AB�ϵ�һ�㣬������A��B�غϣ�������P��AB�Ĵ��߽�BC���ӳ����ڵ�Q��
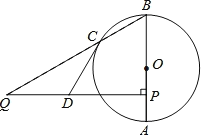
��1����D���߶�PQ�ϣ���DQ=DC����֤��CD����O�����ߣ�
��2����sin��Q=![]() ��BP=6��AP=2����QC�ij���
��BP=6��AP=2����QC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ף���ƽ��ֱ������ϵ�У�ֱ�߷ֱ�![]() �ᡢ
�ᡢ![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ����λ���ȣ���
����λ���ȣ���![]() Ϊֱ��
Ϊֱ��![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ����
����![]() ������
������![]() ��
��![]() ���е�ֱ�Ϊ
���е�ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��
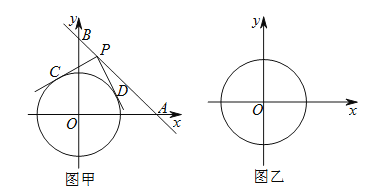
��1���ж��ı���![]() ����״��˵�����ɣ�
����״��˵�����ɣ�
��2�����![]() �����꣮
�����꣮
��3����ֱ��![]() ��
��![]() ������ƽ�Ƶõ�һ���µ�ֱ��
������ƽ�Ƶõ�һ���µ�ֱ��![]() ����ֱ�߽���
����ֱ�߽���![]() ��Բ�ֵܷ����λ���֮��Ϊ
��Բ�ֵܷ����λ���֮��Ϊ![]() ����ֱ��д��
����ֱ��д��![]() ��ֵ��
��ֵ��
��4��������![]() ��
��![]() ������ƽ�ƣ�Բ��
������ƽ�ƣ�Բ��![]() ʼ�ձ�����
ʼ�ձ�����![]() ���ϣ�����д������
���ϣ�����д������![]() ��ֱ��
��ֱ��![]() �н���ʱԲ��
�н���ʱԲ��![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ����ֱ��д���𰸣�
��ȡֵ��Χ����ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪PΪ��ABC��һ�㣬��P��ֱ���ֱ��ƽ������ABC�ĸ��ߣ��γ�С�����ε����S1��S2��S3���ֱ�Ϊ4��9��49������ABC�����Ϊ_____��
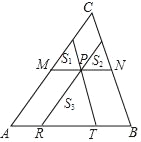
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com