
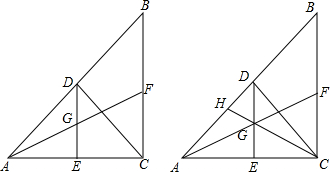
分析 (1)由直角三角形的性质得出∠BAC=∠DCB,由AAS证明△ADE≌△CBD,即可得出∴DE=DB;
(2)证出DE∥BC,由平行线分线段成比例定理得出$\frac{DG}{BF}=\frac{AG}{AF}$,$\frac{AG}{AF}=\frac{GE}{FC}$,证出$\frac{DG}{BF}=\frac{GE}{FC}$,再由已知条件即可得出结论;
(3)连接HF,过H作HM⊥AC于M,连接DM,如图所示:由平行线证出AM=CM=$\frac{1}{2}$AC=2,得出DM=$\frac{1}{2}$AC=2,由三角形中位线定理得出HF∥AC,HF=$\frac{1}{2}$AC,由平行线得出比例式$\frac{AG}{GF}=\frac{AC}{HF}$=2,求出AE=$\frac{2}{3}$AC=$\frac{8}{3}$,得出ME=AE-AM=$\frac{2}{3}$,在Rt△DEM中,由勾股定理求出DE即可.
解答 (1)证明:∵∠ACB=90°,
∴∠B+∠BAC=90°,
∵CD为AB边上的高线,
∴∠CDB=90°,
∴∠DCB+∠B=90°,
∴∠BAC=∠DCB,
∵DE⊥AC,
∴∠DEA=∠CDB=90°,
在△ADE和△CBD中,$\left\{\begin{array}{l}{∠DAE=∠DCB}&{\;}\\{∠DEA=∠CDB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$,
∴△ADE≌△CBD(AAS),
∴DE=DB;
(2)证明:∵∠ACB=90°,
∴BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴$\frac{DG}{BF}=\frac{AG}{AF}$,$\frac{AG}{AF}=\frac{GE}{FC}$,
∴$\frac{DG}{BF}=\frac{GE}{FC}$,
∵G是DE的中点,
∴DG=GE,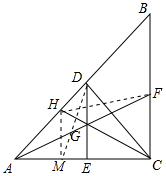
∴BF=FC,
∴F是BC的中点;
(3)解:连接HF,过H作HM⊥AC于M,连接DM,如图所示:
∵HM⊥AC,BC⊥AC,
∴HM∥BC,
∵AH=BH,
∴AM=CM=$\frac{1}{2}$AC=2,
∵CD⊥AB,
∴△ADC是直角三角形,
∴DM=$\frac{1}{2}$AC=2,
∵F是BC中点,
∴HF∥AC,HF=$\frac{1}{2}$AC,
∴$\frac{AG}{GF}=\frac{AC}{HF}$=2,
∴$\frac{AG}{AF}=\frac{AE}{AC}$=$\frac{2}{3}$,
∴AE=$\frac{2}{3}$AC=$\frac{8}{3}$,
∴ME=AE-AM=$\frac{8}{3}$-2=$\frac{2}{3}$,
在Rt△DEM中,DE=$\sqrt{D{M}^{2}-M{E}^{2}}$=$\sqrt{{2}^{2}-(\frac{2}{3})^{2}}$=$\frac{4}{3}$$\sqrt{2}$.
点评 本题是三角形综合题目,考查了全等三角形的判定与性质、平行线的判定、平行线分线段成比例定理、等腰三角形的判定与性质、三角形中位线定理、勾股定理等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+8)=9 | B. | x(8-x)=9 | C. | x(16-x)=9 | D. | x(16-2x)=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图、正比例函数y1=k1x与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于(1,2),则在第一象限内不等式k1x>$\frac{{k}_{2}}{x}$的解集为x>1.
如图、正比例函数y1=k1x与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于(1,2),则在第一象限内不等式k1x>$\frac{{k}_{2}}{x}$的解集为x>1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
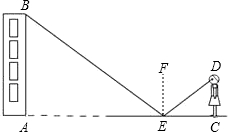 小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com