Question

7．如图，在平面直角坐标系中，点A的坐标是（-3，0），点P是y轴上的一个动点，以AP为边向上方作一等边三角形△APB．

（1）填空：当点B位于x轴上时，点B的坐标是（3，0），当点B位于y轴上时，点B的坐标是（0，$\sqrt{3}$）；
（2）当点P的坐标为（0，2$\sqrt{3}$）时，求OB的值；
（3）通过操作、观察、判断：OB是否存在最小值？若存在，请直接写出OB的最小值；若不存在，试说明理由．

Answer 1

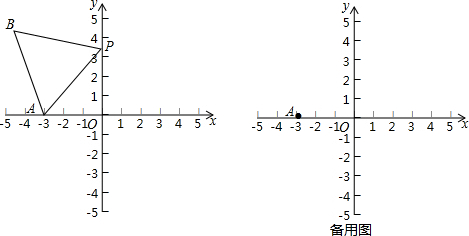
分析 （1）利用等边三角形的性质及x轴与y轴上点的特点求解即可，
（2）在Rt△AOP中，由勾股定理，可得出AP的值，由等边三角形ABP中，AB=BP=AP，设点B坐标为（ a，b ）（b＞0）可得AB²=（a+3）²+b²=21，BP²=a²+（b-2$\sqrt{3}$）²=21可得b的值．进而求出点B坐标，即可求出OB的长．．
（3）存在，OB的最小值为$\frac{3}{2}$； 通过操作、观察知：点B在直线L：$y=-\frac{{\sqrt{3}}}{3}x+\sqrt{3}$上移动，当OB⊥L时，OB取最小值，利用直角三角形即可求出OB的长．

解答 解：（1）当点B位于x轴上时，
∵△APB为等边三角形，
∴点B与点A关于y轴对称，
∴B（3，0），
当点B位于y轴上时，
∵△APB为等边三角形，
∴∠ABO=60°
∴B（0，$\sqrt{3}$）．
故答案为：3，0，0，$\sqrt{3}$．
（2）如图1，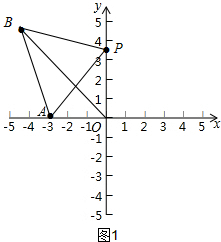

∵A（-3，0），P（0，$2\sqrt{3}$），
∴OA=3，OP=2$\sqrt{3}$，
在Rt△AOP中，由勾股定理，得AP=$\sqrt{O{A}^{2}+O{P}^{2}}$=$\sqrt{21}$，
在等边三角形ABP中，AB=BP=AP=$\sqrt{21}$，设点B坐标为（ a，b ）（b＞0）可得AB²=（a+3）²+b²=21，（Ⅰ）   
BP²=a²+（b-2$\sqrt{3}$）²=21（Ⅱ），
由（Ⅰ）、（Ⅱ）得6a+4$\sqrt{3}$b=3，代入（Ⅰ）或（Ⅱ）可得84b²-168$\sqrt{3}$b-315=0，
解得b₁=$\frac{5\sqrt{3}}{2}$，b₂=-$\frac{\sqrt{3}}{2}$（不合题意，舍去）．
∴点B坐标为（$-\frac{9}{2}$，$\frac{{5\sqrt{3}}}{2}$），
∴OB=$\sqrt{（-\frac{9}{2}）^{2}+（\frac{5\sqrt{3}}{2}）^{2}}$=$\sqrt{39}$．
（3）存在，OB的最小值为$\frac{3}{2}$； 
如图2，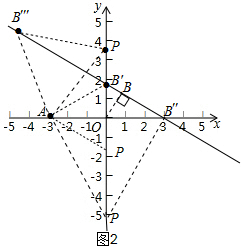

通过操作、观察知：点B在直线L：$y=-\frac{{\sqrt{3}}}{3}x+\sqrt{3}$上移动，
∴当OB⊥L时，OB取最小值，
∴OB=$\frac{3}{2}$．

点评 本题主要考查了点的坐标，等边三角形性质，勾股定理及求最小值等知识，解题的关键是灵活运用等边三角形的性质，培养学生的操作、观察能力．