
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AC��60 cm����A��60������D�ӵ�C������CA������4 cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2 cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t��(0<t��15)������D��DF��BC�ڵ�F������DE��EF��
(1)��֤��AE��DF��
(2)�ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
(3)��tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
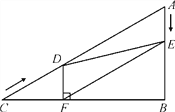
���𰸡�(1)֤����������(2) �ܣ����ɼ�������(3)��������
����������������1������t��ʾ��CD�Լ�AE�ij���Ȼ����ֱ�ǡ�CDF��������ֱ�������ε��������DF�ij�������֤����
��2����֤�ı���AEFD��ƽ���ı�������AD=AEʱ���ı���AEFD���������ݴ˼����з������t��ֵ��
��3��������������ۼ�����⣮
�������1����ֱ�ǡ�ABC������C=90�㩁��A=30�㣮
��CD=4t��AE=2t��
�֡���ֱ�ǡ�CDF������C=30�㣬��DF=![]() CD=2t����DF=AE��
CD=2t����DF=AE��
��2����DF��AB��DF=AE�����ı���AEFD��ƽ���ı�������AD=AEʱ���ı���AEFD����������60��4t=2t�������t=10������t=10ʱ��AEFD��������
��3�����������������
�ٵ���EDF=90��ʱ��DE��BC�����ADE=��C=30�㣬��AD=2AE��
��CD=4t����DF=2t=AE����AD=4t����4t+4t=60����t=![]() ʱ����EDF=90�㣮
ʱ����EDF=90�㣮
�ڵ���DEF=90��ʱ��DE��EF��
���ı���AEFD��ƽ���ı�������AD��EF����DE��AD�����ADE��ֱ������������ADE=90�㣮
�ߡ�A=60�㣬���DEA=30�㣬��AD=![]() AE��AD=AC��CD=60��4t��AE=DF=
AE��AD=AC��CD=60��4t��AE=DF=![]() CD=2t����60��4t=t�����t=12��
CD=2t����60��4t=t�����t=12��
������������t=![]() ��t=12ʱ����DEF��ֱ�������Σ�
��t=12ʱ����DEF��ֱ�������Σ�


 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������������ϸ��Ҫ�������������ϱ��У�430��20��g�������ʣ�
��1��������������ı������Ƕ��٣����ϱ����������������ĺϸ�Χ�Ƕ��٣�
��2����ί����������8ֻ��������������ڱ�������Ϊ�������ڱ�������Ϊ��������ֱ��ǣ���15g��+12g����24g����6g��+13g����5g��+22g����9g������8ֻ���������ĺϸ��ʣ�
�����������ĺϸ���=![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�ȹ۲����е�ʽ��������������:
![]() ��
��![]() ��
��![]()
���������:![]() ��________.
��________.
����a��b����������![]() ��
��
��:![]() +��+
+��+![]() ��ֵ.
��ֵ.
(2)̽�������㣺![]() +
+![]() +
+![]() +��+
+��+![]()
(3)��ͼ����һ�����Ϊ1�������εȷֳ��������Ϊ![]() �ij����Σ����Ű����Ϊ
�ij����Σ����Ű����Ϊ![]() �ij����εȷֳ��������Ϊ
�ij����εȷֳ��������Ϊ![]() �������Σ��ٰ����Ϊ
�������Σ��ٰ����Ϊ![]() �������εȷֳ��������Ϊ
�������εȷֳ��������Ϊ![]() �ľ��Σ���˽�����ȥ��������ͼ�ν�ʾ�Ĺ��ɼ��㣺
�ľ��Σ���˽�����ȥ��������ͼ�ν�ʾ�Ĺ��ɼ��㣺![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() .��ֱ��д�𰸣�.
.��ֱ��д�𰸣�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���A,B�������Ϸֱ��ʾ������a��b��A,B����֮��ľ����ʾΪAB����������A,B�������AB=|a��b|����֪����������A,B��Ӧ�����ֱ�Ϊ-1,3.��PΪ������һ���㣬���Ӧ����Ϊx��A,B����֮��ľ����� .���P�������ϱ�ʾ����Ϊx����x��-4֮��ľ����ʾΪ .
.����P����A����B�ľ�����ȣ����P��Ӧ����Ϊ .
����P����A����B�ľ���֮��Ϊ8�����P��Ӧ����Ϊ .
���ڵ�A��2����λ����/����ٶ������˶���ͬʱ��B��0.5����λ����/����ٶ������˶�������A���B֮��ľ���Ϊ3����λ����ʱ�����A����Ӧ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ӵ�����PQ��MN����ƽ�У��Ӱ�PQ�ϵĵ�A���͵�B������һ�ô�����AB=30�ף�ij���ںӰ�MN��ѡһ��C��AC��MN����ֱ��MN�ϴӵ�Cǰ��һ��·�̵����D����á�ADC=30�㣬��BDC=60�㣬�������ӵĿ��ȣ��� ![]() ��1.732���������������Ч���֣���
��1.732���������������Ч���֣���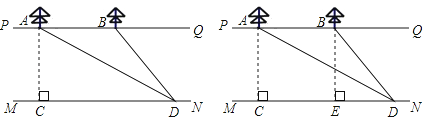
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3cm��EΪCD����һ�㣬��DAE=30����MΪAE���е㣬����M��ֱ�߷ֱ���AD��BC�ཻ�ڵ�P��Q����PQ=AE����AP���� cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ǽ�����ABCD�Ե�OΪ���İ�˳ʱ�뷽��ֱ���ת90����180����270�����γɵ�ͼ�Ρ���![]() ��AB=2����ͼ����Ӱ���ֵ����Ϊ______.
��AB=2����ͼ����Ӱ���ֵ����Ϊ______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2��2x��3��x���ཻ��A��B���㣬�䶥��ΪM��������������x���·��IJ�����x�ᷭ�ۣ����ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ����ͼ����ֱ��y����x��n���ͼ������ֻ������������ʱ����n��ȡֵ��ΧΪ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����10̨A�ͺ�20̨B�͵��Ե�����Ϊ4000Ԫ������20̨A�ͺ�10̨B�͵��Ե�����Ϊ3500Ԫ��
��1����ÿ̨A�͵��Ժ�B�͵��Ե���������
��2�����̵�ƻ�һ�ι��������ͺŵĵ��Թ�100̨������B�͵��ԵĽ�����������A�͵��Ե�2�����蹺��A�͵���x̨����100̨���Ե�����������ΪyԪ�� ����y����x�ĺ�����ϵʽ��
�ڸ��̵깺��A�͡�B�͵��Ը�����̨������ʹ�������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com