
 观察下列各个等式:
观察下列各个等式:分析 (1)根据给定的等式,找出规律“n3-(n-1)3=3n2-3n+1”,将n个等式的左右两边分别相加,通过合并同类项、分解因式即可得出结论;
(2)由二次函数的解析式找出点A、点B的坐标,再根据线段OA的n等分的特点找出各Ak的横坐标、Bk的纵坐标(k为小于n的正整数),结合三角形的面积公式找出Sn的通式,将其相加整理即可得出“S1+S2+…+Sn=$\frac{9(2{n}^{2}+n-1)}{4{n}^{2}}$”,利用该等式即可解决①②两问.
解答 解:(1)观察,发现规律:13-03=3-3+1,23-13=3×22-3×2+1,33-23=3×32-3×3+1,…,
∴n3-(n-1)3=3n2-3n+1.
将这n个等式的左右两边分别相加得:n3=3×(12+22+32+…+n2)-3×(1+2+3+…+n)+n,
即12+22+32+42+…+n2=$\frac{{n}^{3}+3(1+2+3+…+n)-n}{3}$=$\frac{n(n+1)(2n+1)}{6}$.
(2)∵抛物线y=-x2+2x+3=-(x+1)(x-3),
∴点B的坐标为(0,3),点A的坐标为(3,0).
∴点A1、A2、A3、A4、A5、A6、…、An-1的横坐标分别为$\frac{3}{n}、\frac{6}{n}、\frac{9}{n}、…、\frac{3(n-1)}{n}$,
点B1、B2、B3、B4、B5、B6、…、Bn-1的纵坐标分别为$-{(\frac{3}{n})^2}+2(\frac{3}{n})+3、-{(\frac{6}{n})^2}+2(\frac{6}{n})+3、…、-{[\frac{3(n-1)}{n}]^2}+2×\frac{3(n-1)}{n}+3$,
∴${S_1}=\frac{9}{2n},{S_2}=\frac{{9({n^2}+2n-3)}}{{2{n^3}}},{S_3}=\frac{{9({n^2}+4n-12)}}{{2{n^3}}},…,{S_n}=\frac{{9[{n^2}+2({n^2}-n)-3{{(n-1)}^2}]}}{{2{n^3}}}$,
∴${S_1}+{S_2}+{S_3}+…+{S_n}=\frac{{9\{{n^3}+2n(1+2+3+…+n-1)-3[{1^2}+{2^2}+{3^2}+…+{{(n-1)}^2}]\}}}{{2{n^3}}}$=$\frac{9[{n}^{3}+2n×\frac{n(n+1)}{2}-3×\frac{n(n-1)(2n-1)}{6}]}{2{n}^{3}}$=$\frac{9(2{n}^{2}+n-1)}{4{n}^{2}}$.
①当n=2012时,S1+S2+S3+S4+S5+…+S2012=$\frac{72884691}{16192576}$;
②∵${S_1}+{S_2}+{S_3}+…+{S_n}=\frac{{9(2{n^2}+n-1)}}{{4{n^2}}}=\frac{9}{2}+\frac{9}{4n}-\frac{9}{{4{n^2}}}$
∴当n取到无穷无尽时,上式的值等于$\frac{9}{2}$,即所有三角形的面积和等于$\frac{9}{2}$.
点评 本题考查了规律型中的数的变化、三角形的面积公式以及分式的化简求值,解题的关键是:(1)找出规律“n3-(n-1)3=3n2-3n+1”;(2)根据数据的变化找出“S1+S2+…+Sn=$\frac{9(2{n}^{2}+n-1)}{4{n}^{2}}$”.本题属于基础题,难度不大,解决该题型题目时,根据数据的变化找出数据的变化规律是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | l⊥AC | B. | l平分AB | C. | l平分∠C | D. | l平分$\widehat{AB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,-3) | B. | (-2,3) | C. | (-3,2) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.
如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
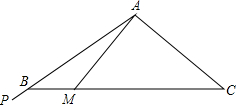 在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.
在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y1<y3<y2 | D. | y2<y3<y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com