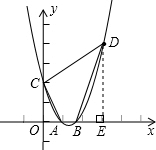
已知在平面直角坐标系中,点C(0,2),D(3,4),在x轴正半轴上有一点A,且它到原点的距离为1.
(1)求过点C、A、D的抛物线的解析式;
(2)设(1)中抛物线与x轴的另一个交点为B,求四边形CABD的面积;
(3)把(1)中的抛物线先向左平移一个单位,再向上或向下平移多少个单位能使抛物线与直线AD只有一个交点?
分析:(1)先设抛物线的解析式,然后将对应的三个点的值代入其中得出常数项的值,即可得到抛物线解析式;
(2)当函数值为0时,可得到抛物线与x轴的两个交点的坐标,故可求出AB的长度,过点D作x轴的垂线,用直角梯形的面积减去直角三角形的面积可得四边形CABD的面积;
(3)先写出向左平移一个单位的抛物线解析式,再设向上或向下平移k个单位的解析式,将其与直线AD的解析式组成一个方程组,解此方程组可得k的值,即再向上或向下平移多少个单位能使抛物线与直线AD只有一个交点.
解答:解:(1)根据题意可知A的坐标为(1,0),
设过C、A、D三点的抛物线的解析式为:y=ax
2+bx+c(a≠0),
∵C(0,2),A(1,0),D(3,4),
∴
,
解得
,
故过C、A、D三点的抛物线的解析式为:
y=x2-x+2;
(2)∵点B为抛物线与x轴的另一个交点,令y=0,
则
x2-x+2=0,
∴
x1=1,x2=,
∴点B的坐标为
(,0),
作DE⊥x轴于点E,
∴S
四边形CABD=S
梯形OEDC-S
△AOC-S
△BDE=5;
(3)把抛物线
y=x2-x+2,
即
y=(x-)2-,
向左平移一个单位得到的抛物线的解析式为:
y=(x-+1)2-,
即
y=x2-x,
设抛物线
y=x2-x向上或向下平移|k|个单位能使抛物线与直线AD只有一个交点,
则向上或向下平移|k|个单位抛物线的解析式为:
y=x2-x+k,
设过A、D两点的解析式为y=ax+b,
∵A(1,0),D(3,4),
代入上式得
,
解得
,
∴直线AD的解析式为:y=2x-2,
得
,
∴4x
2-8x+3k+6=0,
∴△=64-16(3k+6)=0,
解得,k=-
,
即抛物线
y=x2-x向下平移
个单位,与直线AD只有一个交点.
点评:本题主要考查二次函数的综合运用,其中涉及四边形的面积,三角形的面积及抛物线的平移.




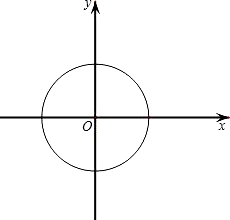 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1. 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.