
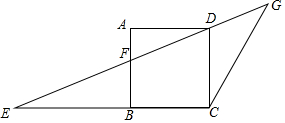
 如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.
如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.分析 (1)根据正方形的性质得到∠A=∠ABC=∠ABE=90°,根据相似三角形的判定定理即可得到结论;
(2)如图,作GH⊥EC,垂足为H,得到BF∥CD∥HG,根据平行线分线段成比例定理得到$\frac{EF}{DF}=\frac{BE}{BC}$=2,得到BE=10,求得CE=15,根据相似三角形的性质得到GH=$\frac{20}{3}$,由三角形的面积公式即可得到结论.
解答 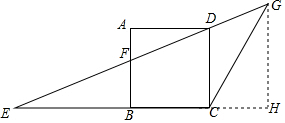 (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠ABE=90°,
∴∠FAD=∠FBE=90°,
∵∠GFB=∠DFA,
∴△FAD∽△FBE;
(2)解:如图,作GH⊥EC,垂足为H,
则BF∥CD∥HG,
∴$\frac{EF}{DF}=\frac{BE}{BC}$=2,
∴BE=10,
∴CE=15,
∵CD∥HG,
∴△CDE∽△HGE,
∴$\frac{CD}{GH}$=$\frac{DE}{EG}$,即$\frac{5}{GH}$=$\frac{3}{4}$,
∴GH=$\frac{20}{3}$,
∴△ECG的面积=$\frac{1}{2}$CE•GH=$\frac{1}{2}×$15×$\frac{20}{3}$=50.
点评 本题考查了相似三角形的判定和性质,正方形的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
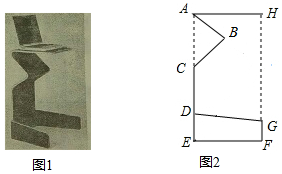 如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.
如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.| 获奖等级 | 频数 |
| 一等奖 | a |
| 二等奖 | b |
| 三等奖 | 275 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com