
若⊙O的直径是4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是__.
相离 【解析】r=2,d=3, 则直线l与⊙O的位置关系是相离科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:单选题
在下列式子中变形正确的是( )
A. 如果 =
=  ,那么
,那么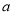 +
+ 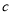 =
=  ﹣
﹣ B. 如果
B. 如果 =
=  ,那么
,那么 C. 如果
C. 如果 ﹣
﹣ +
+  =0,那么
=0,那么 =
=  +
+  D. 如果
D. 如果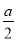 =4,那么
=4,那么 =2
=2
查看答案和解析>>
科目:初中数学 来源:云南省双柏县2017-2018学年八年级上期期末数学试卷 题型:填空题
下列实数中,无理数有( )个
 ,π,
,π, 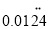 ,0.1212212221…(相邻两个1之间2的个数逐次加1)
,0.1212212221…(相邻两个1之间2的个数逐次加1)
A. 1 B. 2 C. 3 D. 4
B 【解析】【解析】 无理数有:π,0.1212212221…(相邻两个1之间2的个数逐次加1),共2个,故选B.查看答案和解析>>
科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:解答题
初三(1)班要从2男2女共4名同学中选人做晨会的升旗手.
(1)若从这4人中随机选1人,则所选的同学性别为男生的概率是 .
(2)若从这4人中随机选2人,求这2名同学性别相同的概率.
(1);(2)P(这2名同学性别相同) =. 【解析】试题分析:(1)用男生人数2除以总人数4即可得出答案; (2)根据题意先画出树状图,得出所有情况数,再根据概率公式即可得出答案. 【解析】 (1); (2)从4人中随机选2人,所有可能出现的结果有:(男1,男2)、(男1,女1)、(男1,女2)、(男2,男1)、(男2,女1)、(男2,女2)、(女1,男1)、(女1,男...查看答案和解析>>
科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD:AB=4:9,则S△ADE:S△ABC= .
查看答案和解析>>
科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:单选题
八年级某同学6次数学小测验的成绩分别为:80分,85分,95分,95分,95分,100分,则该同学这6次成绩的众数和中位数分别是( )
A.95分,95分 B.95分,90分 C. 90分,95分 D.95分,85分
A. 【解析】 试题分析:这组数据中95出现了3次,次数最多,为众数;中位数为第3和第4两个数的平均数为95,故选A.查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型:解答题
甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
(1)树状图见解析;(2). 【解析】试题分析:先根据题意画树状图,再根据所得结果计算两个数字之和能被3整除的概率. 试题解析:(1)树状图如下: (2)∵共6种情况,两个数字之和能被3整除的情况数有2种, ∴两个数字之和能被3整除的概率为, 即P(两个数字之和能被3整除)=.查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型:单选题
△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
C 【解析】【解析】 ∵△ABC与△DEF的相似比为1:4,∴△ABC与△DEF的周长比为1:4.故选C.查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,四边形ABCD中,AB∥CD,过点D作DF⊥BC,垂足为F,DF与AC交于点M,已知∠1=∠2.
(1)求证:CM=DM;
(2)若FB=FC,求证:AM-MD=2FM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com