
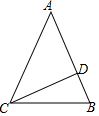
 从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.
从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.分析 (1)根据题意画出图形,运用三角形内角和定理,即可得到顶点对应角的度数;
(2)根据△CBD∽△ABC,得到$\frac{BD}{BC}$=$\frac{CD}{AB}$,再设BD=x,则$\frac{x}{1}$=$\frac{1}{x+1}$,即x2+x+1=0,即可解得x=$\frac{\sqrt{5}-1}{2}$,进而得到BD=$\frac{\sqrt{5}-1}{2}$;
(3)过点C作CE⊥AB交AB于点E,根据等腰三角形的性质可得BE=$\frac{1}{2}$BD=$\frac{\sqrt{5}-1}{4}$,在Rt△BCE中,根据勾股定理可得CE=$\sqrt{C{B}^{2}-B{E}^{2}}$=$\frac{\sqrt{10+2\sqrt{5}}}{4}$,最后在Rt△BCE中,求得sin72°=$\frac{CE}{CB}$=$\frac{\sqrt{10+2\sqrt{5}}}{4}$.
解答 解:(1)符合条件的三角形可画出如下三种: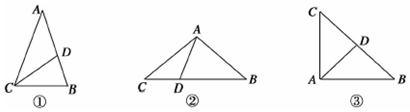
如图①,△BCD∽△BAC,△ACD是等腰三角形,
设∠A=∠ACD=α,则∠BDC=∠B=2α,∠BCD=α,
∵△BCD的内角和等于180°,
∴5α=180°,即α=36°,
∴∠ACB=72°;
如图②,△CAD∽△CBA,△BAD是等腰三角形,
设∠C=∠CAD=α,则∠ADB=∠DAB=2α,∠B=α,
∵△ADB的内角和等于180°,
∴5α=180°,即α=36°,
∴∠CAB=3α=108°;
如图③,△CAD∽△CBA,△BAD是等腰三角形,
设∠C=∠B=∠CAD=α,则∠ADB=2α,∠DAB=α,
∵△ADB的内角和等于180°,
∴4α=180°,即α=45°,
∴∠BAD=2α=90°,
综上所述,这个顶点对应角的度数分别为72°,108°,90°;
(2)由题意知,△CBD∽△ABC,
∴$\frac{BD}{BC}$=$\frac{CD}{AB}$,
设BD=x,则
$\frac{x}{1}$=$\frac{1}{x+1}$,即x2+x+1=0,
解得x=$\frac{\sqrt{5}-1}{2}$,
∴BD=$\frac{\sqrt{5}-1}{2}$;
(3)如图所示,过点C作CE⊥AB交AB于点E,
则BE=$\frac{1}{2}$BD=$\frac{\sqrt{5}-1}{4}$,
∴Rt△BCE中,CE=$\sqrt{C{B}^{2}-B{E}^{2}}$=$\sqrt{1-(\frac{\sqrt{5}-1}{4})^{2}}$=$\frac{\sqrt{10+2\sqrt{5}}}{4}$,
∴Rt△BCE中,sin72°=$\frac{CE}{CB}$=$\frac{\sqrt{10+2\sqrt{5}}}{4}$.
点评 本题主要考查了相似三角形的性质,等腰三角形的性质,黄金分割以及三角形内角和定理的综合应用,解题时注意分类思想的运用.解决问题的关键是画出图形,依据等腰三角形和相似三角形的性质进行求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
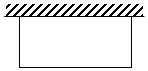 用28米长的铁丝围成一个一边靠墙的长方形.
用28米长的铁丝围成一个一边靠墙的长方形.| 垂直于墙的一边比另一边少(m) | 1 | 4 | 7 | 10 | 13 |
| 长方形的面积 | 90 | 96 | 98 | 96 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
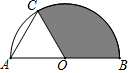 如图,AB是半圆O的直径,点C在半圆O上,且△OAC是等边三角形,若AB=12,则图中阴影部分图形的面积为( )
如图,AB是半圆O的直径,点C在半圆O上,且△OAC是等边三角形,若AB=12,则图中阴影部分图形的面积为( )| A. | 12π | B. | 8π | C. | 24π | D. | 16π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=5}\\{y=6}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=5}\\{y=10}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=10}\\{y=15}\end{array}}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com