
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?

【答案】(1)60.(2)y乙=90x﹣90;y甲=60x.()220km
【解析】
(1)根据图象确定出甲的路程与时间,即可求出速度;
(2)利用待定系数法即可解决问题;
(3)求出乙距A地240km时的时间,加上1,再乘以甲的速度即可得到结果.
(1)根据图象得:360÷6=60km/h.
故答案为:60.
(2)当1≤x≤5时,设y乙=kx+b,把(1,0)与(5,360)代入得: ,解得:k=90,b=﹣90,则y乙=90x﹣90;
,解得:k=90,b=﹣90,则y乙=90x﹣90;
当0<x≤6时,设y甲=mx,把(6,360)代入得到m=60,∴y甲=60x.
(3)∵乙与A地相距240km,且乙的速度为360÷(5﹣1)=90km/h,∴乙用的时间是240÷90= h,则甲与A地相距60×(
h,则甲与A地相距60×( +1)=220km.
+1)=220km.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
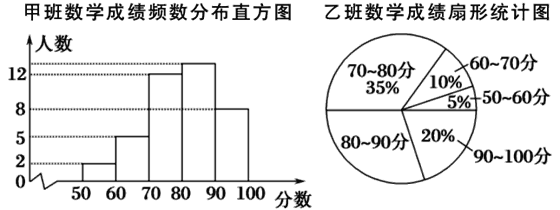
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
查看答案和解析>>
科目:初中数学 来源: 题型:
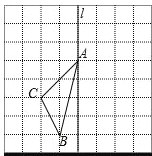
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PB+PC的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
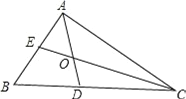
【题目】如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
(1)求∠AOC的度数;
(2)求证:OE=OD;
(3).猜测AE,CD,AC三者的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线经过坐标原点O,点A(6,﹣6 ![]() ),且以y轴为对称轴.
),且以y轴为对称轴.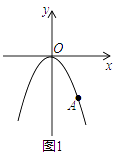
(1)求抛物线的解析式;
(2)如图2,过点B(0,﹣ ![]() )作x轴的平行线l,点C在直线l上,点D在y轴左侧的抛物线上,连接DB,以点D为圆心,以DB为半径画圆,⊙D与x轴相交于点M,N(点M在点N的左侧),连接CN,当MN=CN时,求锐角∠MNC的度数;
)作x轴的平行线l,点C在直线l上,点D在y轴左侧的抛物线上,连接DB,以点D为圆心,以DB为半径画圆,⊙D与x轴相交于点M,N(点M在点N的左侧),连接CN,当MN=CN时,求锐角∠MNC的度数;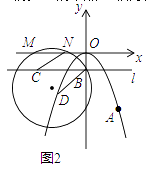
(3)如图3,在(2)的条件下,平移直线CN经过点A,与抛物线相交于另一点E,过点A作x轴的平行线m,过点(﹣3,0)作y轴的平行线n,直线m与直线n相交于点S,点R在直线n上,点P在EA的延长线上,连接SP,以SP为边向上作等边△SPQ,连接RQ,PR,若∠QRS=60°,线段PR的中点K恰好落在抛物线上,求Q点坐标.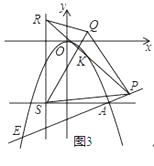
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O是△ABC的外接圆,AB是直径,过 ![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP; 
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG; 
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ![]() ,求AC的长.
,求AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
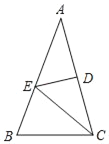
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com