
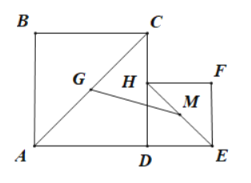
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬AB=8£¬BC=12£¬EŹĒBC±ßµÄÖŠµć£¬µćPŌŚĻ߶ĪADÉĻ£¬¹żP×÷PF”ĶAEÓŚF£¬ÉčPA=x£®
£Ø1£©ĒóÖ¤£ŗ”÷PFA”×”÷ABE£»
£Ø2£©µ±µćPŌŚĻ߶ĪADÉĻŌĖ¶ÆŹ±£¬ŹĒ·ń“ęŌŚŹµŹżx£¬Ź¹µĆŅŌµćP£¬F£¬EĪŖ¶„µćµÄČż½ĒŠĪŅ²Óė”÷ABEĻąĖĘ£æČō“ęŌŚ£¬ĒėĒó³öxµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©Ģ½¾æ£ŗµ±ŅŌDĪŖŌ²ŠÄ£¬DPĪŖ°ė¾¶µÄ”ŃDÓėĻ߶ĪAEÖ»ÓŠŅ»øö¹«¹²µćŹ±£¬ĒėÖ±½ÓŠ“³öDPĀś×ćµÄĢõ¼ž£ŗ”” ””£®
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©“ęŌŚ£¬Āś×ćĢõ¼žµÄxµÄÖµĪŖ6»ņ![]() £»£Ø3£©DP=
£»£Ø3£©DP=![]() »ņ10£¼DP”Ü12
»ņ10£¼DP”Ü12
”¾½āĪö”æ
£Ø1£©øł¾Ż¾ŲŠĪµÄŠŌÖŹ£¬½įŗĻŅŃÖŖĢõ¼žæÉŅŌÖ¤Ć÷Į½øö½Ē¶ŌÓ¦ĻąµČ£¬“Ó¶ųÖ¤Ć÷Čż½ĒŠĪĻąĖĘ£»
£Ø2£©ÓÉÓŚ¶ŌÓ¦¹ŲĻµ²»Č·¶Ø£¬ĖłŅŌÓ¦Õė¶Ō²»Ķ¬µÄ¶ŌÓ¦¹ŲĻµ·ÖĒéæöæ¼ĀĒ£ŗ¢Łµ±”ĻPEF=”ĻEABŹ±£¬ŌņµĆµ½ĖıߊĪABEPĪŖ¾ŲŠĪ£¬“Ó¶ųĒóµĆxµÄÖµ£»¢Śµ±”ĻPEF=”ĻAEBŹ±£¬ŌŁ½įŗĻ£Ø1£©ÖŠµÄ½įĀŪ£¬µĆµ½µČŃü”÷APE£®ŌŁøł¾ŻµČŃüČż½ĒŠĪµÄČżĻßŗĻŅ»µĆµ½FŹĒAEµÄÖŠµć£¬ŌĖÓĆ¹“¹É¶ØĄķŗĶĻąĖĘČż½ĒŠĪµÄŠŌÖŹ½ųŠŠĒó½ā£®
£Ø3£©Ź×ĻČ¼ĘĖćŌ²DÓėĻ߶ĪĻąĒŠŹ±£¬xµÄÖµ£¬ŌŚ»³öŌ²D¹żEŹ±£¬°ė¾¶rµÄÖµ£¬Č·¶ØxµÄÖµ£¬°ė¾¶±ČÕāŹ±“󏱷ūŗĻĢāŅā£¬øł¾ŻĶ¼ŠĪČ·¶ØxµÄȔֵ·¶Ī§,“Ó¶ųµĆ³öDPµÄ·¶Ī§£®
£Ø1£©Ö¤Ć÷£ŗ”ß¾ŲŠĪABCD£¬
”ą”ĻABE=90”ć£¬AD”ĪBC£¬
”ą”ĻPAF=”ĻAEB£¬
ÓÖ”ßPF”ĶAE£¬
”ą”ĻPFA=90”ć=”ĻABE£¬
”ą”÷PFA”×”÷ABE£®
£Ø2£©½ā£ŗ·Ö¶žÖÖĒéæö£ŗ
¢ŁČō”÷EFP”×”÷ABE£¬ČēĶ¼1£¬
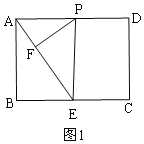
Ōņ”ĻPEF=”ĻEAB£¬
”ąPE”ĪAB£¬
”ąĖıߊĪABEPĪŖ¾ŲŠĪ£¬
”ąPA=EB=6£¬¼“x=6£®
¢ŚČēĶ¼2£¬Čō”÷PFE”×”÷ABE£¬

Ōņ”ĻPEF=”ĻAEB£¬
”ßAD”ĪBC
”ą”ĻPAF=”ĻAEB£¬
”ą”ĻPEF=”ĻPAF£®
”ąPE=PA£®
”ßPF”ĶAE£¬
”ąµćFĪŖAEµÄÖŠµć£¬
Rt”÷ABEÖŠ£¬AB=8£¬BE=6£¬
”ąAE=![]() =
=![]() =10£¬
=10£¬
”ąEF=![]() £¬
£¬
”ß”÷PFE”×”÷ABE£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ąPE=![]() £¬
£¬
”ąĀś×ćĢõ¼žµÄxµÄÖµĪŖ6»ņ![]() £®
£®
£Ø3£©ČēĶ¼3£¬µ±”ŃDÓėAEĻąĒŠŹ±£¬ÉčĒŠµćĪŖG£¬Į¬½ÓDG£¬
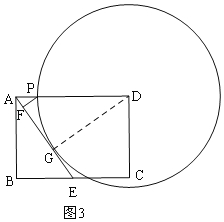
”ßAP=x£¬
”ąPDØTDG=12©x£¬
”ß”ĻDAG=”ĻAEB£¬”ĻAGD=”ĻB=90”ć£¬
”ą”÷AGD”×”÷EBA£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ąx=![]() £¬
£¬
”ą![]() £¬
£¬
µ±”ŃD¹żµćEŹ±£¬ČēĶ¼4£¬”ŃDÓėĻ߶ĪÓŠĮ½øö¹«¹²µć£¬Į¬½ÓDE£¬
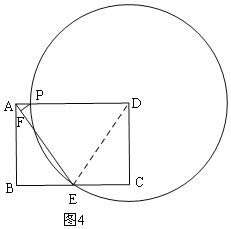
“ĖŹ±PD=DE=10£¬
¹Ź“š°øĪŖ£ŗDP=![]() »ņ10£¼DP”Ü12£®
»ņ10£¼DP”Ü12£®


 »ĘøŌ¹Ś¾üæĪæĪĮ·ĻµĮŠ“š°ø
»ĘøŌ¹Ś¾üæĪæĪĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬ŅŃÖŖ”ĻACB£½90”ć£¬”ĻA£½30”ć£¬BC£½6£¬DĪŖŠ±±ßABÉĻŅ»µć£¬ŅŌCD”¢CBĪŖ±ß×÷Ę½ŠŠĖıߊĪCDEB£¬µ±AD£½_____Ź±£¬Ę½ŠŠĖıߊĪCDEBĪŖĮāŠĪ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÖŠ£¬”ĻC=90”ć£¬AD”ĶDB£¬µćEĪŖABµÄÖŠµć£¬DE”ĪBC£®
£Ø1£©ĒóÖ¤£ŗBDĘ½·Ö”ĻABC£»
£Ø2£©Į¬½ÓEC£¬Čō”ĻA=30”ć£¬DC![]() £¬ĒóECµÄ³¤£®
£¬ĒóECµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() ,µć
,µć![]() ĪŖ
ĪŖ![]() ÉĻµÄŅ»µć£¬ŌŚ
ÉĻµÄŅ»µć£¬ŌŚ![]() Ķ¬²ą×÷Õż·½ŠĪ
Ķ¬²ą×÷Õż·½ŠĪ![]() ,Õż·½ŠĪ
,Õż·½ŠĪ![]() ·Ö±šĪŖ¶Ō½ĒĻß
·Ö±šĪŖ¶Ō½ĒĻß![]() µÄÖŠµć£¬Į¬½į
µÄÖŠµć£¬Į¬½į![]() µ±µć
µ±µć![]() ŃŲ×ÅĻ߶Ī
ŃŲ×ÅĻ߶Ī![]() Óɵć
Óɵć![]() Ļņµć
Ļņµć![]() ·½ĻņÉĻŅĘ¶ÆŹ±£¬ĖıߊĪ
·½ĻņÉĻŅĘ¶ÆŹ±£¬ĖıߊĪ![]() µÄĆ껿±ä»ÆĒéæöĪŖ( )
µÄĆ껿±ä»ÆĒéæöĪŖ( )
A.²»±äB.ĻČ¼õŠ”ŗóŌö“ó
C.ĻČŌö“óŗó¼õŠ”D.Ņ»Ö±¼õŠ”
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµŲĒųŌŚŅ»“Ī¾ÅÄź¼¶ŹżŃ§×öĮĖ¼ģ²āÖŠ£¬ÓŠŅ»µĄĀś·Ö8·ÖµÄ½ā“šĢā£¬°“ĘĄ·Ö±ź×¼£¬ĖłÓŠæ¼ÉśµÄµĆ·ÖÖ»ÓŠĖÄÖÖ£ŗ0·Ö£¬3·Ö£¬5·Ö£¬8·Ö£®ĄĻŹ¦ĪŖĮĖĮĖ½āѧɜµÄµĆ·ÖĒéæöÓėĢāÄæµÄÄŃŅ×Ēéæö£¬“ÓČ«Ēų4500Ćūæ¼ÉśµÄŹŌ¾ķÖŠĖ껜³éČ”Ņ»²æ·Ö£¬Ķعż·ÖĪöÓėÕūĄķ£¬»ęÖĘĮĖČēĻĀĮ½·łĶ¼²»ĶźÕūµÄĶ³¼ĘĶ¼£®
Ēėøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĢīæÕ£ŗa=””””£¬b=””””£¬²¢°ŃĢõŠĪĶ³¼ĘĶ¼²¹Č«£»
£Ø2£©Ēė¹Ą¼ĘøƵŲĒų“ĖĢāµĆĀś·Ö£Ø¼“8·Ö£©µÄѧɜČĖŹż£»
£Ø3£©ŅŃÖŖÄѶČĻµŹżµÄ¼ĘĖć¹«Ź½ĪŖL=![]() £¬ĘäÖŠLĪŖÄѶČĻµŹż£¬XĪŖŃł±¾Ę½¾łµĆ·Ö£¬WĪŖŹŌĢāĀś·ÖÖµ£®Ņ»°ćĄ“Ėµ£¬øł¾ŻŹŌĢāµÄÄѶČĻµŹżæɽ«ŹŌĢā·ÖĪŖŅŌĻĀČżĄą£ŗµ±0£¼L”Ü0.4Ź±£¬“ĖĢāĪŖÄŃĢā£»µ±0.4£¼L”Ü0.7Ź±£¬“ĖĢāĪŖÖŠµČÄѶȏŌĢā£»µ±0.7£¼L£¼1Ź±£¬“ĖĢāĪŖČŻŅ×Ģā£®ŹŌĪŹ“ĖĢā¶ŌÓŚøƵŲĒųµÄ¾ÅÄź¼¶Ń§ÉśĄ“ĖµŹōÓŚÄÄŅ»Ąą£æ
£¬ĘäÖŠLĪŖÄѶČĻµŹż£¬XĪŖŃł±¾Ę½¾łµĆ·Ö£¬WĪŖŹŌĢāĀś·ÖÖµ£®Ņ»°ćĄ“Ėµ£¬øł¾ŻŹŌĢāµÄÄѶČĻµŹżæɽ«ŹŌĢā·ÖĪŖŅŌĻĀČżĄą£ŗµ±0£¼L”Ü0.4Ź±£¬“ĖĢāĪŖÄŃĢā£»µ±0.4£¼L”Ü0.7Ź±£¬“ĖĢāĪŖÖŠµČÄѶȏŌĢā£»µ±0.7£¼L£¼1Ź±£¬“ĖĢāĪŖČŻŅ×Ģā£®ŹŌĪŹ“ĖĢā¶ŌÓŚøƵŲĒųµÄ¾ÅÄź¼¶Ń§ÉśĄ“ĖµŹōÓŚÄÄŅ»Ąą£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ”ĒųÓĪÓ¾¹ŻĻļ¾ĶĘ³öĮ½ÖÖŹÕ·Ń·½Ź½£®·½Ź½Ņ»£ŗĻČ¹ŗĀņ»įŌ±Ö¤£¬»įŌ±Ö¤200ŌŖ£¬Ö»ĻŽ±¾ČĖµ±ÄźŹ¹ÓĆ£¬Ę¾Ö¤ÓĪÓ¾Ćæ“ĪŠčĮķø¶·Ń10ŌŖ£ŗ·½Ź½¶ž£ŗ²»¹ŗĀņ»įŌ±Ö¤£¬Ćæ“ĪÓĪÓ¾Ščø¶·Ń20ŌŖ£®
£Ø1£©Čō¼×¼Ę»®½ńÄźĻļ¾ÓĪÓ¾µÄ·ŃÓĆĪŖ500ŌŖ£¬ŌņŃ”ŌńÄÄÖÖø¶·Ń·½Ź½ÓĪÓ¾“ĪŹż±Č½Ļ¶ą£æ
£Ø2£©ČōŅŅ¼Ę»®½ńÄźĻļ¾ÓĪÓ¾µÄ“ĪŹż³¬¹ż15“Ī£¬ŌņŃ”ŌńÄÄÖÖø¶·Ń·½Ź½ÓĪÓ¾»Ø·Ń±Č½ĻÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³ÖŠŃ§ĪŖ·įø»Ń§ÉśµÄŠ£Ō°Éś»ī£¬×¼±ø“ÓĢåÓżÓĆĘ·ÉĢµźŅ»“ĪŠŌ¹ŗĀņČōøÉøö×ćĒņŗĶĄŗĒņ£ØĆæøö×ćĒņµÄ¼ŪøńĻąĶ¬£¬ĆæøöĄŗĒņµÄ¼ŪøńĻąĶ¬£©£¬Čō¹ŗĀņ3øö×ćĒņŗĶ2øöĄŗĒņ¹²Šč310ŌŖ£¬¹ŗĀņ2øö×ćĒņŗĶ5øöĄŗĒņ¹²Šč500ŌŖ”£
£Ø1£©Ēó¹ŗĀņŅ»øö×ćĒņ”¢Ņ»øöĄŗĒņø÷Šč¶ąÉŁŌŖ£æ
£Ø2£©øł¾ŻŃ§Š£Źµ¼ŹĒéæö£¬Šč“ÓĢåÓżÓĆĘ·ÉĢµźŅ»“ĪŠŌ¹ŗĀņ×ćĒņŗĶĄŗĒņ¹²96øö£¬ŅŖĒó¹ŗĀņ×ćĒņŗĶĄŗĒņµÄ×Ü·ŃÓĆ²»³¬¹ż5720ŌŖ£¬ÕāĖłÖŠŃ§×ī¶ąæÉŅŌ¹ŗĀņ¶ąÉŁøöĄŗĒņ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßy£½![]() x+2ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćC£®Å×ĪļĻßy£½ax2+bx+cµÄ¶Ō³ĘÖįŹĒx£½©
x+2ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćC£®Å×ĪļĻßy£½ax2+bx+cµÄ¶Ō³ĘÖįŹĒx£½©![]() ĒŅ¾¹żA”¢CĮ½µć£¬ÓėxÖįµÄĮķŅ»½»µćĪŖµćB£®
ĒŅ¾¹żA”¢CĮ½µć£¬ÓėxÖįµÄĮķŅ»½»µćĪŖµćB£®
£Ø1£©¢ŁÖ±½ÓŠ“³öµćBµÄ×ų±ź£»¢ŚĒóÅ×ĪļĻß½āĪöŹ½£®
£Ø2£©ČōµćPĪŖÖ±ĻßACÉĻ·½µÄÅ×ĪļĻßÉĻµÄŅ»µć£¬Į¬½ÓPA£¬PC£®Ēó”÷PACµÄĆ껿µÄ×ī“óÖµ£¬²¢Ēó³ö“ĖŹ±µćPµÄ×ų±ź£®
£Ø3£©Å×ĪļĻßÉĻÓŠŅ»µćM£¬¹żµćM×÷MN“¹Ö±xÖįÓŚµćN£¬Ź¹µĆŅŌµćA”¢M”¢NĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬Ö±½ÓŠ“³öµćMµÄ×ų±ź£®
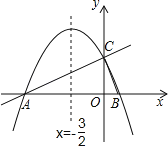
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=2xÓėŗÆŹży=![]() £Øx£¾0£©µÄĶ¼Ļó½»ÓŚµćA£Ø1£¬2£©£®
£Øx£¾0£©µÄĶ¼Ļó½»ÓŚµćA£Ø1£¬2£©£®
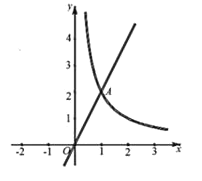
£Ø1£©ĒómµÄÖµ£»
£Ø2£©¹żµćA×÷xÖįµÄĘ½ŠŠĻßl£¬Ö±Ļßy=2x+bÓėÖ±Ļßl½»ÓŚµćB£¬ÓėŗÆŹży=![]() £Øx£¾0£©µÄĶ¼Ļó½»ÓŚµćC£¬ÓėxÖį½»ÓŚµćD£®
£Øx£¾0£©µÄĶ¼Ļó½»ÓŚµćC£¬ÓėxÖį½»ÓŚµćD£®
¢ŁČōµćCŹĒĻ߶ĪBDµÄÖŠµćŹ±£¬ŌņµćCµÄ×ų±źŹĒ________£¬bµÄÖµŹĒ________£»
¢Śµ±BC£¾BDŹ±£¬Ö±½ÓŠ“³öbµÄȔֵ·¶Ī§________£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com