
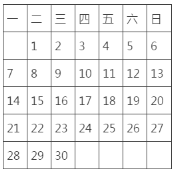
【题目】如图,是某年11月月历
(1)用一个正方形在表中随意框住4个数,把其中最小的记为![]() ,则另外三个可用含
,则另外三个可用含![]() 的式子表示出来,从小到大依次为____________,_____________,_______________.
的式子表示出来,从小到大依次为____________,_____________,_______________.
(2)在(1)中被框住的4个数之和等于76时,则被框住的4个数分别是多少?
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取了一个班学生的成绩进行整理,分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
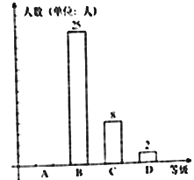
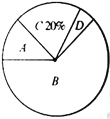
(1)请估计本校初三年级等级为![]() 的学生人数;
的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某商场用2800元从厂家购进A、B两种纪念品共50件,其中A种纪念品进价为每件80元,B种纪念品进价为每件40元.求A、B两种纪念品各购进多少件?
(2)商场要再次购进A、B两种纪念品共200件,若进价不变,且A种纪念品以每件110元售出,B种纪念品以每件55元售出.在购买这些纪念品的资金不超过12120元,且售完这些纪念品的利润不少于4500元的情况下,该商场共有几种进货方案?
请一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月11日24时,天猫双11成交额达到2684亿元.同一天,各电商平台上众品牌网上促销如火如荼,纷纷推出多种销售玩法吸引顾客让利消费者.某品牌标价每件100元的商品就推出了如下的优惠促销活动
一次性购物总金额 | 优惠措施 |
少于或等于700元 | 一律打八折 |
超过700元,但不超过900元 | 一律打六折 |
超过900元 | 其中900元部分打五折, 超过900元的部分打三折优惠 |
(1)王教授一次性购买该商品12件,实际付款________元.
(2)李阿姨一次性购买该商品若干件,实际付款480元,请认真思考求出李阿姨购买该商品的件数的所有可能.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲三角形的周长为![]() ,乙三角形的第一条边长为
,乙三角形的第一条边长为![]() ,第二条边长为
,第二条边长为![]() ,第三条边比第二条边短
,第三条边比第二条边短![]() .
.
(1)求乙三角形第三条边的长;
(2)甲三角形和乙三角形的周长哪个大?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的位置如图所示(每个小方格都是边长1个单位长度的正方形).
的位置如图所示(每个小方格都是边长1个单位长度的正方形).
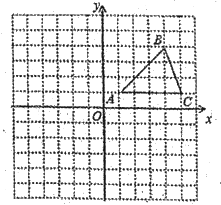
(1)将![]() 沿
沿![]() 轴方向向左平移6个单位,画出平移后得到的
轴方向向左平移6个单位,画出平移后得到的![]() .
.
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ;直接写出点
;直接写出点![]() 的坐标.
的坐标.
(3)作出![]() 关于原点
关于原点![]() 成中心对称的
成中心对称的![]() ,并直接写出
,并直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
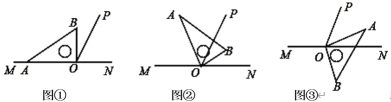
【题目】已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,将一块直角三角板的直角顶点始终放在点O处.
(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,求∠POB的度数;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,求∠BOP和∠AOM 的度数;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,若OP所在的直线平分∠MOB,求∠POA 的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com