
【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).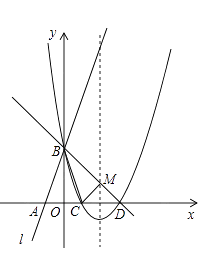
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
【答案】
(1)解:∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,

∴A(﹣1,0),B(0,3);
∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴ ![]() ,
,
解得k=﹣1,b=3,
∴直线BD的解析式为:y=﹣x+3.
设抛物线的解析式为:y=a(x﹣1)(x﹣3),
∵点B(0,3)在抛物线上,
∴3=a×(﹣1)×(﹣3),
解得:a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3
(2)解:抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).
直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MF=1,
∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
如答图1所示:

(I)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(﹣3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,﹣3).
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3)
(3)解:方法一:
假设存在点P,使S△PBD=6,设点P坐标为(m,n).
(I)当点P位于直线BD上方时,如答图2所示:

过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3.
S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE= ![]() (3+n)m﹣
(3+n)m﹣ ![]() ×3×3﹣
×3×3﹣ ![]() (m﹣3)n=6,
(m﹣3)n=6,
化简得:m+n="7" ①,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入①式整理得:m2﹣3m﹣4=0,
解得:m1=4,m2=﹣1,
∴n1=3,n2=8,
∴P1(4,3),P2(﹣1,8);
(II)当点P位于直线BD下方时,如答图3所示:

过点P作PE⊥y轴于点E,则PE=m,OE=﹣n,BE=3﹣n.
S△PBD=S梯形PEOD+S△BOD﹣S△PBE= ![]() (3+m)(﹣n)+
(3+m)(﹣n)+ ![]() ×3×3﹣
×3×3﹣ ![]() (3﹣n)m=6,
(3﹣n)m=6,
化简得:m+n=﹣1 ②,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).
方法二:
假设存在点P,使S△PBD=6,
过点P作直线l平行BD,则l与BD的距离为d,
∵BD= ![]() =3
=3 ![]() ,
,
∴S△PBD= ![]() BD×d,
BD×d,
∴d=2 ![]() ,
,
∵BD与y轴夹角为45°,
∴BB′=4,
∴将BD上移或下移4个单位,
①上移4个单位,l解析式为:y=﹣x+7,
∵y=x2﹣4x+3,
∴x2﹣3x﹣4=0,
∴x1=4,x2=﹣1,
②下移4个单位,l解析式为y=﹣x﹣1,
∵y=x2﹣4x+3,
∴x2﹣3x+4=0,△<0,∴此方程无解,
综上所述,点P的坐标为(4,3)或(﹣1,8)
【解析】(1)由题意得到A、B的坐标,由△AOB沿y轴翻折,得到C点坐标,由B、D点坐标求出直线BD的解析式;由点B坐标得到二次函数解析式;(2)由抛物线的解析式,得到顶点坐标,由已知条件得到△MCD为等腰直角三角形,由点N、B、D为顶点的三角形与△MCD相似,得到△BND为等腰直角三角形,(I)若BD为斜边,则易知此时直角顶点为原点O,得到点N的坐标;(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,得到点N的坐标;(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,得到点N的坐标;(3)(I)当点P位于直线BD上方时,求出S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE的值,得到点P的坐标;(II)当点P位于直线BD下方时,求出S△PBD=S梯形PEOD+S△BOD﹣S△PBE的值,得到此时点P不存在;此题是综合题,难度较大,计算和解方程时需认真仔细.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的.如图的统计图反映了不同捐款数的人数比例,那么该班同学平均每人捐款( )
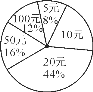
A. 32.4元 B. 31.2元 C. 31元 D. 32元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩 (百分制) | 面试 | 86 | 92 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们![]() 和
和![]() 的权.根据四人各自的平均成绩,公司将录取( )
的权.根据四人各自的平均成绩,公司将录取( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实行中考改革,需要根据该市中学体能的实际情况重新制定中考体育标准.为此,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试.测试的情况绘制成表格如下:
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少?
次数 | 6 | 12 | 15 | 18 | 20 | 25 | 27 | 30 | 32 | 35 | 36 |
人数 | 1 | 1 | 7 | 18 | 10 | 5 | 2 | 2 | 1 | 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简
(1)![]() ; (2)(﹣2a2)(3ab2﹣5ab3)
; (2)(﹣2a2)(3ab2﹣5ab3)
(3)(x+3)(x﹣7)﹣x(x﹣1). (4)(a﹣2b+1)(a+2b+1)
(5)(3a﹣b)2﹣(2a+b)2﹣5a(a﹣b) (6)(x+2y)2(x﹣2y)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com