

 解:
解: =2
=2
 )
) ,OC=OB1cos60°=1
,OC=OB1cos60°=1 )
) ),B1(1,
),B1(1, )代入得
)代入得

 x2+
x2+ x.
x. x2+
x2+ x的对称轴是x=-
x的对称轴是x=- ,
, 对称的点是B2(-
对称的点是B2(- ,
, ),
), ,
, )代入得
)代入得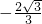 ,
,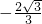 x
x 时,y=
时,y= ,
, ,
, )使PO+PB1的值最小.
)使PO+PB1的值最小.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
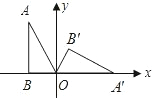 如图Rt△ABO中,∠A=30°,OB=2,如果将Rt△ABO在坐标平面内,绕原点O按顺时针方向旋转到OA′B′的位置.
如图Rt△ABO中,∠A=30°,OB=2,如果将Rt△ABO在坐标平面内,绕原点O按顺时针方向旋转到OA′B′的位置.查看答案和解析>>
科目:初中数学 来源:2009年浙江省宁波市江北区中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:内蒙古自治区中考真题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com