
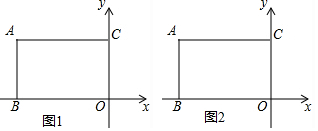
���� ��1�����ݾ��ε����ʡ����ͼ�ν��
��2������ƽ�ƹ�������ͼ�Σ����ݾ��ε������ʽ���㼴�ɣ�
��3���ֵ�P���߶�O��C���Ϻ͵�P���߶�A��C����������������������ε������ʽ���㼴�ɣ�
���  �⣺��1�����ݾ��ε����ʿ�֪��A������Ϊ��-6��4����
�⣺��1�����ݾ��ε����ʿ�֪��A������Ϊ��-6��4����
�ʴ�Ϊ����-6��4����
��2��ƽ�ƺ��ͼ����ͼ1��ʾ��
������ABOC�볤����A��B��O��C���ص����ֵ����Ϊ��4��2=8��
��3������P���߶�O��C�����ƶ�ʱ��
��O��P=x����C��P=4-x��
������ã� 4��6-$\frac{1}{2}$��3��4-$\frac{1}{2}$��3��x-$\frac{1}{2}$��6����4-x��=8��
4��6-$\frac{1}{2}$��3��4-$\frac{1}{2}$��3��x-$\frac{1}{2}$��6����4-x��=8��
��ã�x=$\frac{4}{3}$��
��t=$\frac{4}{3}$��
����P���߶�A��C�����ƶ�ʱ��
��A��P��=y��
������ã�$\frac{1}{2}$��y��4=8��
��ã�y=4��
��A��P��=4��P��C��=2��
��t=6��
�𣺵�t=$\frac{4}{3}$��6��ʱ��������A��EP�������8����ʱ��P������Ϊ��-2��-$\frac{2}{3}$����-4��2����
���� ���⿼����Ǿ��ε����ʡ������ε������ʽ�Լ�������ͼ�ε����������վ��ε������ǽ���Ĺؼ������ʱ��ע����������˼���������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ�������������������������ǻ�Ϊ�෴�� | |
| B�� | ����û�������� | |
| C�� | �κ�һ���������������ǷǸ��� | |
| D�� | ������һ��������������������һ������������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com