
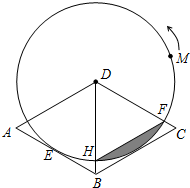
 如图,在菱形ABCD中,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.
如图,在菱形ABCD中,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.分析 (1)连接DE,过D作DN垂直于BC,垂足为N,由四边形ABCD为菱形,且∠A=60°,利用菱形的性质得到BD为角平分线,且三角形ABD与三角形DBC都为等边三角形,进而确定出BE=BN,利用SAS得到三角形DBE与三角形DBN全等,利用全等三角形对应边相等得到DN=DE,进而得到DN垂直于BC,即可得证;
(2)由题意求出AD与AE的长,利用勾股定理求出DE长,即为圆的半径,判断得到三角形HDF为等边三角形,由阴影部分面积=扇形DHF面积-三角形DHF面积,求出即可;
(3)假设点M运动到某一位置时,满足题意,过M点作MP⊥DF于点P,分别表示出三角形MDF与三角形ABD面积,根据面积之比表示出MP,根据DM=r得出三角形DPM为等腰直角三角形,求出∠MDP=45°,由圆的对称性可知,这样的点M有四个不同位置,分别求出各自的弧长,即为动点M经过的弧长.
解答 (1)证明:连结DE,过点D作DN⊥BC,垂足为点N,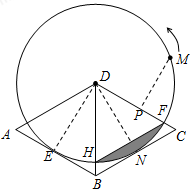
∵四边形ABCD为菱形,∠A=60°,
∴BD平分∠ABC,即∠DBE=∠DBN,△ABD与△DBC都为等边三角形,
∴EB=NB=$\frac{1}{2}$AB=$\frac{1}{2}$BC,
∵边AB与⊙D相切于点E,
∴DE⊥AB,
在△DBE和△DBN中,
$\left\{\begin{array}{l}{DB=DB}\\{∠DBE=∠DBN}\\{BE=BN}\end{array}\right.$,
∴△DBE≌△DBN(SAS),
∴DN=DE,DN⊥BC,
∴⊙D与边BC也相切;
(2)解:∵四边形ABCD为菱形,AB=$\sqrt{3}$,
∴AD=$\sqrt{3}$,
∴DE=$\sqrt{(\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}}$=$\frac{3}{2}$,即⊙D的半径是$\frac{3}{2}$,
又∵∠HDF=$\frac{1}{2}$∠CDA=60°,DH=DF,
∴△HDF是等边三角形,
∵S△HDF=$\frac{1}{2}$DB•DC•sin∠DBC=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{3}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{16}$,S扇形HDF=$\frac{60π×(\frac{3}{2})^{2}}{360}$=$\frac{3π}{8}$,
∴S阴影=S扇形HDF-S△HDF=$\frac{3π}{8}$-$\frac{9\sqrt{3}}{16}$;
(3)解:假设点M运动到某一位置时,满足题意,过M点作MP⊥DF于点P,
∵S△ABD=$\frac{1}{2}$r•$\frac{2}{\sqrt{3}}$r=$\frac{\sqrt{3}}{3}$r2,S△MDF=$\frac{1}{2}$r•MP,
且△MDF与△ABD的面积之比为$\sqrt{3}$:2$\sqrt{2}$,
∴($\frac{1}{2}$r•MP):($\frac{\sqrt{3}}{3}$r2)=$\sqrt{3}$:2$\sqrt{2}$,
整理得:MP=$\frac{\sqrt{2}}{2}$r,
又DM=r,
∴PD=$\frac{\sqrt{2}}{2}$r,
∴∠MDP=45°,
由圆的对称性可知,这样的点M有四个不同位置,
此时经过点M的弧长依次为:$\frac{π}{4}$r,$\frac{3π}{4}$r,$\frac{5π}{4}$r,$\frac{7π}{4}$r,
综上所述,动点M经过的弧长依次为:$\frac{π}{4}$r,$\frac{3π}{4}$r,$\frac{5π}{4}$r,$\frac{7π}{4}$r.
点评 此题属于圆综合题,涉及的知识有:全等三角形的判断与性质,菱形的性质,等边三角形的判定与性质,扇形面积公式,以及弧长公式,熟练掌握性质及公式是解本题的关键.


科目:初中数学 来源: 题型:解答题
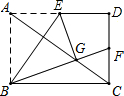 如图,在矩形ABCD中,点E为AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形ABCD的对角线AC上,延长BG交CD于F,连接EF.求$\frac{BE}{EF}$的值.
如图,在矩形ABCD中,点E为AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形ABCD的对角线AC上,延长BG交CD于F,连接EF.求$\frac{BE}{EF}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com