
【题目】在平面直角坐标系中,A(-2,0) ,B(-1,2) ,C(1,0) ,连接 AB,点 D 为 AB 的中点,连接 OB 交 CD于点 E,则四边形 DAOE 的面积为( )
A. 1. B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】根据中点公式求出点D的坐标,然后用待定系数法求出直线OB和直线CD的解析式,将两个解析式联立,求出点E的坐标,然后根据S四边形DAOE=S△DAC-S△EOC计算即可.
如图,

设OB的解析式为y=kx.
将B(-1,2)的坐标代入
得2=-k,解得k=-2.
∴OB的解析式为y=-2x.
∵D为AB的中点,设D(m,n).
∵A(-2,0) ,B(-1,2) ,
∴m=![]() ,n=
,n=![]() .
.
∴D (![]() ,1),
,1),
设CD的解析式为y=ax+b
将C(1,0),D (![]() ,1)的坐标分别代入
,1)的坐标分别代入
得 ,解得
,解得 ,
,
∴CD的解析式为![]() .
.
由 ,得
,得 ,
,
∴![]() ,
,
∵AC=1-(-2)=3,点D (![]() ,1)到AC轴的距离为1.
,1)到AC轴的距离为1.
∴![]() ,
,
∵OC=1,点![]() 到OC的距离为
到OC的距离为![]() .
.
∴![]() ,
,
∴S四边形DAOE=S△DAC-S△EOC=![]() .
.
即四边形DAOE的面积为![]() .
.
故选:C.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. 
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
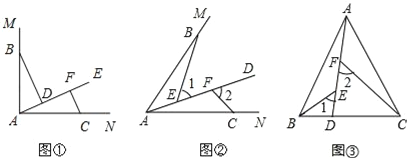
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界杯”期间,某娱乐场所举办“消夏看球赛”活动,需要对会场进行布置,计划在现场安装小彩灯和大彩灯.已知安装5个小彩灯和4个大彩灯共需150元;安装7个小彩灯和6个大彩灯共需220元.
(1)安装1个小彩灯和1个大彩灯各需多少元?
(2)若场地共需安装小彩灯和大彩灯300个,费用不超过4350元,则最多安装大彩灯多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
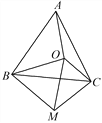
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一次函数y= ![]() x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= ![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= ![]() x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com