
【题目】(12分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由.
(2)若AC=3,∠B=30°,①求⊙O的半径;②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和π)

【答案】(1)相切 (2)半径:2 面积: ![]()
【解析】试题分析:
(1)连结OD,根据平行线判定推出OD∥AC,推出OD⊥BC,根据切线的判定推出即可;
(2)①根据含有30°角的直角三角形的性质得出OB=2OD=2r,AB=2AC=3r,从而求得半径r的值;②根据S阴影=S△BOD-S扇形DOE求得即可.
试题解析:(1)相切.理由如下:
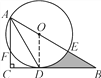
如图,连接OD.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵OA=OD,∴∠ODA=∠BAD,∴∠ODA=∠CAD,∴OD∥AC.又∠C=90°,∴OD⊥BC,∴BC与⊙O相切.
(2)①在Rt△ACB和Rt△ODB中,
∵AC=3,∠B=30°,∴AB=6,OB=2OD.
又OA=OD=r,∴OB=2r,∴2r+r=6,解得r=2,即⊙O的半径是2.
②由①得OD=2,则OB=4,BD=2![]() ,
,
S阴影=S△BDO-S扇形CDE=![]() ×2
×2![]() ×2-
×2-![]() =2
=2![]() -
-![]() π.
π.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.

(1)求抛物线的表达式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com