
����Ŀ����ͼ�٣���O��������ABCD���Խ��ߵĽ��㣬�ֱ��ӳ�OD����G��OC����E��ʹOG��2OD��OE��2OC��Ȼ����OG��OEΪ�ڱ���������OEFG������AG��DE.
(1)��֤��DE��AG��
(2)������ABCD�̶�����������OEFG�Ƶ�O��ʱ����ת����(0��������360��)�õ�������OE��F��G������ͼ��.
������ת�����У�����OAG����ֱ��ʱ�������Ķ�����
����������ABCD�ı߳�Ϊ1������ת�����У���AF���������ֵ�ʹ�ʱ���Ķ�����ֱ��д���������˵�����ɣ�

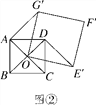
���𰸡���1�������� ����2��������30����150�� ��������315��.
���������������: ��1���ӳ�ED��AG�ڵ�H����֤��AOG�ա�DOE���õ���AGO=��DEO��Ȼ�����õ�������֤����AHE=90�㼴�ɣ�
��2��������ת�����У���OAG���Ϊֱ�����������������0������90������У�����OAG��=90��ʱ����=30�㣬����90������180������У�����OAG��=90��ʱ����=150�㣻
�ڵ���ת��A��O��F����һ��ֱ����ʱ��AF��ij����AF��=AO+OF��=![]() +2����ʱ��=315�㣮
+2����ʱ��=315�㣮
�������:
(1)��ͼ1,�ӳ�ED��AG�ڵ�H,
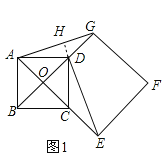
�ߵ�O��������ABCD���Խ��ߵĽ��㣬
��OA=OD��OA��OD��
��OG=OE��
����AOG����DOE��
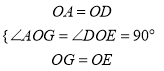 ��
��
����AOG����DOE��
���AGO=��DEO��
�ߡ�AGO+��GAO=90����
���GAO+��DEO=90����
���AHE=90����
��DE��AG��
(2)������ת������,��OAG����Ϊֱ�������������
(��)����0������90��������,����OAG��=90��ʱ��
��OA=OD=![]() OG=
OG=![]() OG����
OG����
����Rt��OAG����,sin��AG��O=![]() =
=![]() ��
��
���AG��O=30����
��OA��OD,OA��AG����
��OD��AG��,
���DOG��=��AG��O=30����
����=30����
(��)����90������180��������,����OAG��=90��ʱ��
ͬ�������BOG��=30����
����=180��30��=150��.
��������,����OAG��=90��ʱ,��=30����150��.
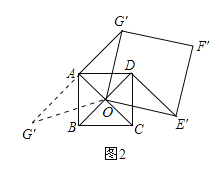
����ͼ3,����ת��A.O��F����һ��ֱ����ʱ,AF���ij����
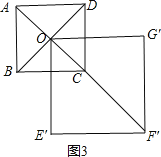
��������ABCD�ı߳�Ϊ1��
��OA=OD=OC=OB=![]() ��
��
��OG=2OD��
��OG��=OG=![]() ��
��
��OF��=2��
��AF��=AO+OF��=![]() +2��
+2��
�ߡ�COE��=45����
���ʱ��=315��.
�㾦: ���⿼����������ε����ʡ���ת�任�������Լ�������Ǻ����Ķ��壬���������ε���������ȡ��ĸ�����ȣ���ת�任�������ǽ���Ĺؼ���ע������ǵ����Ǻ���ֵ��Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
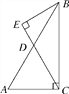
����Ŀ����ͼ����ABC�У���ACB��90����sinA��![]() ��BC��8����D��AB���е㣬����B��CD�Ĵ��ߣ�����Ϊ��E.
��BC��8����D��AB���е㣬����B��CD�Ĵ��ߣ�����Ϊ��E.
(1)���߶�CD�ij���
(2)��cos��ABE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�������ε����߳�Ϊ5��10��������ߵij�����Ϊ��������
A. 5B. 10C. 15D. 20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��m2-3m+2��x|m|-3�Ƿ�������������m��ֵ�ǣ� ��
A.1
B.-2
C.��2
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ�E��F�ֱ���DC��CB���ӳ����ϵĵ㣬��DE��BF������AE��AF��EF.
(1)��֤����ADE�ա�ABF��
(2)��ABF�����ɡ�ADE����ת����________�㣬��˳ʱ����ת________�ȵõ���
(3)��BC��8��DE��6�����AEF�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г����������¼�Ϊ����¼����ǣ� ��
A.ˮ�Ǵ���
B.�������
C.ˮ������
D.Եľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ���2x+a��4=0�Ľ���x=��2����a��ֵ���ڣ� ��
A.��8
B.0
C.2
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��x ��2mx(mΪ����)������1��x��2ʱ������y����СֵΪ��2����m��ֵ��(����)
A. ![]() B.
B. ![]() C.
C. ![]() ��
��![]() D. ��
D. ��![]() ��
��![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com