
【题目】已知BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①所示,试说明OB∥AC;
(2)如图②,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可);
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(4)在(3)的条件下,在平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA的度数等于________(在横线上填上答案即可).
【答案】 见解析 40° (3) 1∶2.(4) 60°
【解析】试题分析:(1)由BC∥OA得∠B+∠O=180°,所以∠O=180°-∠B=80°,则∠A+∠O=180°,根据平行线的判定即可得到OB∥AC;
(2)由OE平分∠BOF得到∠BOE=∠FOE,加上∠FOC=∠AOC,所以∠EOF+∠COF=![]() ∠AOB=40°;
∠AOB=40°;
(3)由BC∥OA得到OCB=∠AOC,∠OFB=∠AOF,加上∠FOC=∠AOC,则∠AOF=2∠AOC,所以∠OFB=2∠OCB,
(4)设∠AOC的度数为x,则∠OFB=2x,根据平行线的性质得∠OEB=∠AOE,则∠OEB=∠EOC+∠AOC=40°+x,再根据三角形内角和定理得∠OCA=180°-∠AOC-∠A=80°-x,利用∠OEB=∠OCA得到40°+x=80°-x,解得x=20°,所以∠OCA=80°-x=60°.
试题解析:(1)∵BC∥OA,
∴∠B+∠O=180°,
∵∠A=∠B,
∴∠A+∠O=180°,
∴OB∥AC;
(2)∵∠A=∠B=100°,由(1)得∠BOA=180°-∠B=80°,
∵∠FOC=∠AOC,OE平分∠BOF,
∴∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,
∠FOA,
∴∠EOC=∠EOF+∠FOC=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ∠BOA=40°,
∠BOA=40°,
故答案为:40°;
(3)∠OCB∶∠OFB的值不发生变化,理由如下:
∵BC∥OA,
∴∠OFB=∠FOA,∠OCB=∠AOC.
∵∠FOC=∠AOC,
∴∠FOC=∠OCB,
∴∠OFB=∠FOA=∠FOC+∠AOC=2∠OCB,
∴∠OCB∶∠OFB=1∶2;
(4)由(1)知OB∥AC,
∴∠OCA=∠BOC,由(2)可设∠BOE=∠EOF=α,∠FOC=∠AOC=β,
∴∠OCA=∠BOC=2α+β,∵BC∥OA,
∴∠OEB=∠EOA=α+2β,
∵∠OEB=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵∠AOB=80°,
∴α=β=20°,
∴∠OCA=2α+β=40°+20°=60°.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
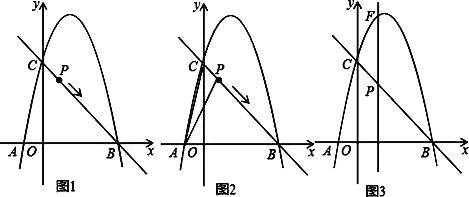
【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒![]() 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2009年1 月的利润为200万元.设2009年1 月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2009年1 月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).

⑴分别求该化工厂治污期间及治污改造工程完工后y与x之间对应的函数关系式.
⑵治污改造工程完工后经过几个月,该厂月利润才能达到2009年1月的水平?
⑶当月利润少于100万元时为该厂资金紧张期,问该厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)、如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD °.
(2)、如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)、在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
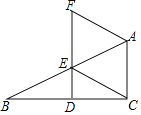
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有公路l1同侧、l2异侧的两个城镇A,B,电信部门要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)中日钓鱼岛争端持续,我海监船加大钓鱼岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.

(1)请用直尺和圆规作出C处的位置;
(2)求我国海监船行驶的航程BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com