
【题目】已知:如图,在平面直角坐标系xoy中,一次函数y= ![]() x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.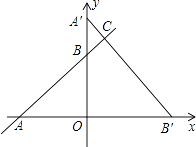
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△ABC:S△ABO的值.
【答案】
(1)解:根据y= ![]() x+3,解得点坐标A(﹣4,0),B(0,3),即OA=4,OB=3,
x+3,解得点坐标A(﹣4,0),B(0,3),即OA=4,OB=3,
∴OA′=OA=4,OB′=OB=3,
∴A′(0,4),B′(3,0),
设直线A′B′的解析式为y=kx+b,则 ![]() ,解得
,解得 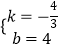 ,
,
∴直线A′B′的解析式为y=﹣ ![]() +4;
+4;
(2)解:解方程组  ,
,
求得两直线交点坐标,得C( ![]() ,
, ![]() ),
),
∴S△A′BC=1× ![]() =
= ![]() ,S△ABO=4×3×
,S△ABO=4×3× ![]() =6,
=6,
∴ ![]() =
= ![]() .
.
【解析】(1)抓住已知将△AOB绕点O顺时针旋转90°后得到△A′OB′.根据旋转的性质得出OA′=OA,OB′=OB,先求出直线AB与两坐标轴的交点坐标,即可得出点A′,B′的坐标,利用待定系数法就可以求出直线A′B′的解析式。
(2)先根据两函数解析式联立方程组,求出方程组的解,即点C的坐标,就可以求出△A′BC和△ABO的面积,即可求出它们的面积之比。
【考点精析】本题主要考查了确定一次函数的表达式和三角形的面积的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能正确解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,双曲线
中,双曲线 ![]() 与直线
与直线 ![]() 交于点A(3,1).
交于点A(3,1).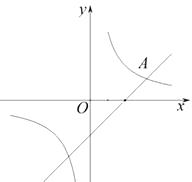
(1)求直线和双曲线的解析式;
(2)直线 ![]() 与x轴交于点B,点P是双曲线
与x轴交于点B,点P是双曲线 ![]() 上一点,过点P作直线PC∥x轴,交y轴于点C,交直线
上一点,过点P作直线PC∥x轴,交y轴于点C,交直线 ![]() 于点D.若DC=2OB,直接写出点
于点D.若DC=2OB,直接写出点 ![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
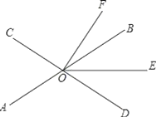
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,△ABC中, ![]() ,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;
,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;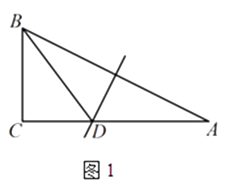
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求 ![]() 的度数;
的度数;
③若 ![]() ,则
,则 ![]() 的值为 .
的值为 . 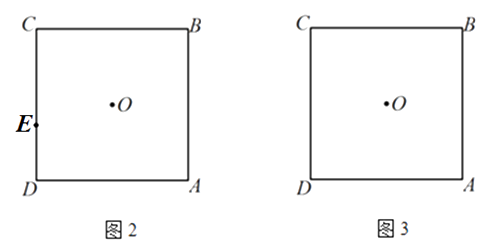
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.3m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据:![]() ≈1.7)
≈1.7)
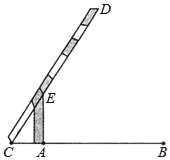
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率= ![]() =
= ![]() ).
).
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com