
”¾ĢāÄæ”æij°ą”°ŹÖĄŹÖ”±ŹżŃ§Ń§Ļ°»„ÖśŠ”×é¶Ō¾ŲŠĪÄŚĮ½Ģõ»„Ļą“¹Ö±µÄĻ߶ĪÓė¾ŲŠĪĮ½ĮŚ±ßµÄŹżĮæ¹ŲĻµ½ųŠŠĢ½¾æŹ±£¬Óöµ½ŅŌĻĀĪŹĢā£¬ĒėÄćÖšŅ»¼ÓŅŌ½ā“š£ŗ
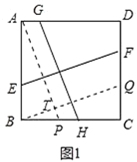
£Ø1£©ČēĶ¼1£¬Õż·½ŠĪABCDÖŠ£¬EF”ĶGH£¬EF·Ö±š½»AB£¬CDÓŚµćE£¬F£¬GH·Ö±š½»AD£¬BCÓŚµćG£¬H£¬ŌņEF”” ””GH£»£ØĢī”°£¾”±”°=”±»ņ”°£¼”±£©
£Ø2£©ČēĶ¼2£¬¾ŲŠĪABCDÖŠ£¬EF”ĶGH£¬EF·Ö±š½»AB£¬CDÓŚµćE£¬F£¬GH·Ö±š½»AD£¬BCÓŚµćG£¬H£¬ĒóÖ¤£ŗ![]() =
=![]() £»
£»
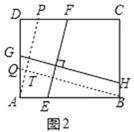
£Ø3£©ČēĶ¼3£¬ĖıߊĪABCDÖŠ£¬”ĻABC=”ĻADC=90”ć£¬BC=3£¬CD=5£¬AD=7£®5£¬AM”ĶDN£¬µćM£¬N·Ö±šŌŚ±ßBC£¬ABÉĻ£¬Ēó![]() µÄÖµ£®
µÄÖµ£®

”¾“š°ø”æ£Ø1£©=£»£Ø2£©¼ū½āĪö£»£Ø3£©![]()
”¾½āĪö”æ
£Ø1£©Ź×ĻČ¹żµćA×÷AP”ĪGH£¬½»BCÓŚP£¬¹żµćB×÷BQ”ĪEF£¬½»CDÓŚQ£¬½»BQÓŚT£¬Č»ŗóøł¾ŻÕż·½ŠĪµÄŠŌÖŹŅŌ¼°”÷ABP”Õ”÷BCQµÄÅŠ¶ØÓėŠŌÖŹ£¬¼“æÉµĆ³öEF=GH£»
£Ø2£©Ź×ĻČ¹żµćA×÷AP”ĪEF£¬½»CDÓŚP£¬¹żµćB×÷BQ”ĪGH£¬½»ADÓŚQ£¬Č»ŗóøł¾Ż¾ŲŠĪµÄŠŌÖŹŅŌ¼°”÷PDA”×”÷QABµÄÅŠ¶ØÓėŠŌÖŹ£¬¼“æÉµĆ³ö![]() £»
£»
£Ø3£©Ź×ĻČ¹żµćD×÷Ę½ŠŠÓŚABµÄÖ±Ļߣ¬½»¹żµćAĘ½ŠŠÓŚBCµÄÖ±ĻßÓŚR£¬½»BCµÄŃÓ³¤ĻßÓŚS£¬ÅŠ¶ØĘ½ŠŠĖıߊĪABSRŹĒ¾ŲŠĪ£¬ÓÉ£Ø1£©½įĀŪµĆ³ö![]() £¬Č»ŗóÅŠ¶Ø”÷ARD”×”÷DSC£¬ŌĖÓĆĘäŠŌÖŹŗĶ¹“¹É¶ØĄķ¹¹½Ø·½³Ģ£¬Ēó½ā¼“æÉ.
£¬Č»ŗóÅŠ¶Ø”÷ARD”×”÷DSC£¬ŌĖÓĆĘäŠŌÖŹŗĶ¹“¹É¶ØĄķ¹¹½Ø·½³Ģ£¬Ēó½ā¼“æÉ.
£Ø1£©ČēĶ¼1ÖŠ£¬¹żµćA×÷AP”ĪGH£¬½»BCÓŚP£¬¹żµćB×÷BQ”ĪEF£¬½»CDÓŚQ£¬½»BQÓŚT£¬
”ßĖıߊĪABCDŹĒÕż·½ŠĪ£¬
”ąAB”ĪDC£¬AD”ĪBC£¬AB=BC£¬”ĻABP=”ĻC=90”ć
”ąĖıߊĪBEFQ”¢ĖıߊĪPHGA¶¼ŹĒĘ½ŠŠĖıߊĪ£¬
”ąAP=GH£¬EF=BQ£®
ÓÖ”ßGH”ĶEF£¬
”ąAP”ĶBQ£¬
”ą”ĻPBT+”ĻABT=90”ć£¬”ĻABT+”ĻBAT=90”ć£¬
”ą”ĻCBQ=”ĻBAT£¬
ŌŚ”÷ABPŗĶ”÷BCQÖŠ£¬
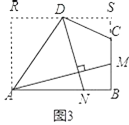
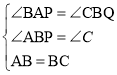 £¬
£¬
”ą”÷ABP”Õ”÷BCQ£¬
”ąAP=BQ£¬
”ąEF=GH£¬
¹Ź“š°øĪŖ£ŗ=£»
£Ø2£©¹żµćA×÷AP”ĪEF£¬½»CDÓŚP£¬¹żµćB×÷BQ”ĪGH£¬½»ADÓŚQ£¬ČēĶ¼2£¬
”ßĖıߊĪABCDŹĒ¾ŲŠĪ£¬
”ąAB”ĪDC£¬AD”ĪBC£®
”ąĖıߊĪAEFP”¢ĖıߊĪBHGQ¶¼ŹĒĘ½ŠŠĖıߊĪ£¬
”ąAP=EF£¬GH=BQ£®
ÓÖ”ßGH”ĶEF£¬
”ąAP”ĶBQ£¬
”ą”ĻQAT+”ĻAQT=90”ć£¬
”ßĖıߊĪABCDŹĒ¾ŲŠĪ£¬
”ą”ĻDAB=”ĻD=90”ć£¬
”ą”ĻDAP+”ĻDPA=90”ć£¬
”ą”ĻAQT=”ĻDPA£¬
”ą”÷PDA”×”÷QAB£¬
”ą![]() £¬
£¬
”ą![]()
![]() £»
£»
£Ø3£©¹żµćD×÷Ę½ŠŠÓŚABµÄÖ±Ļߣ¬½»¹żµćAĘ½ŠŠÓŚBCµÄÖ±ĻßÓŚR£¬½»BCµÄŃÓ³¤ĻßÓŚS£¬ČēĶ¼3£¬
ŌņĖıߊĪABSRŹĒĘ½ŠŠĖıߊĪ£®
”ß”ĻABC=90”ć£¬
”ąĘ½ŠŠĖıߊĪABSRŹĒ¾ŲŠĪ£¬
”ą”ĻR=”ĻS=90”ć£¬RS=AB=10£¬AR=BS£®
”ßAM”ĶDN£¬
”ąÓÉ£Ø1£©ÖŠµÄ½įĀŪæɵĆ![]() £¬
£¬
ÉčSC=x£¬ŌņAR=BS=3+x£¬
”ß”ĻADC=”ĻR=”ĻS=90”ć£¬
”ą”ĻADR+”ĻRAD=90”ć£¬”ĻADR+”ĻSDC=90”ć£¬
”ą”ĻRAD=”ĻCDS£¬
”ą”÷ARD”×”÷DSC£¬
”ą![]() =
=![]() =
=![]() £¬
£¬
”ąDR=![]() x£¬DS=
x£¬DS=![]() £Øx+3£©£¬
£Øx+3£©£¬
ŌŚRt”÷ARDÖŠ£¬”ßAD2=AR2+DR2£¬
”ą7.52=£Øx+3£©2+£Ø![]() x£©2£¬
x£©2£¬
ÕūĄķµĆ13x2+24x©189=0£¬½āµĆx=3»ņ©![]() £¬
£¬
”ąAR=6£¬AB=RS=![]() £¬
£¬
”ą![]() =
=![]() .
.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŹĒÉĻŗ£ŹĄ²©Ō°ÄŚµÄŅ»øö¾ŲŠĪ»ØŌ°£¬»ØŌ°³¤ĪŖ100Ć×£¬æķĪŖ50Ć×£¬ŌŚĖüµÄĖĽĒø÷½ØÓŠŅ»øöĶ¬Ńł“󊔵ÄÕż·½ŠĪ¹Ū¹āŠŻĻ¢Ķ¤£¬ĖÄÖܽØÓŠÓė¹Ū¹āŠŻĻ¢Ķ¤µČæķµÄ¹Ū¹ā“óµĄ£¬ĘäÓą²æ·Ö£ØĶ¼ÖŠŅõÓ°²æ·Ö£©ÖÖÖ²µÄŹĒ²»Ķ¬»Ø²Ż£®ŅŃÖŖÖÖÖ²»Ø²Ż²æ·ÖµÄĆ껿ĪŖ3600Ć×2£¬ÄĒĆ“¾ŲŠĪ»ØŌ°ø÷½Ē“¦µÄÕż·½ŠĪ¹Ū¹āŠŻĻ¢Ķ¤µÄ±ß³¤ĪŖ¶ąÉŁĆ×£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¼Ę»®Ņ»“ĪŠŌ¹ŗĀņÅÅĒņŗĶĄŗĒņ£¬ĆæøöĄŗĒņµÄ¼Ūøń±ČÅÅĒņ¹ó30ŌŖ£»¹ŗĀņ2øöÅÅĒņŗĶ3øöĄŗĒņ¹²Šč340ŌŖ£®
(1)ĒóĆæøöÅÅĒņŗĶĄŗĒņµÄ¼Ūøń£ŗ
(2)ČōøĆŠ£Ņ»“ĪŠŌ¹ŗĀņÅÅĒņŗĶĄŗĒņ¹²60øö£¬×Ü·ŃÓĆ²»³¬¹ż3800ŌŖ£¬ĒŅ¹ŗĀņÅÅĒņµÄøöŹżÉŁÓŚ39øö£®ÉčÅÅĒņµÄøöŹżĪŖm£¬×Ü·ŃÓĆĪŖyŌŖ£®
¢ŁĒóy¹ŲÓŚmµÄŗÆŹż¹ŲĻµŹ½£¬²¢ĒómæÉČ”µÄĖłÓŠÖµ£»
¢ŚŌŚŃ§Š£°“ŌõŃłµÄ·½°ø¹ŗĀņŹ±£¬·ŃÓĆ×īµĶ£æ×īµĶ·ŃÓĆĪŖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬µćF“ÓĮāŠĪABCDµÄ¶„µćA³ö·¢£¬ŃŲA”śD”śBŅŌ1cm/sµÄĖŁ¶ČŌČĖŁŌĖ¶Æµ½µćB£¬Ķ¼2ŹĒµćFŌĖ¶ÆŹ±£¬”÷FBCµÄĆ껿y£Øcm2£©Ėꏱ¼äx£Øs£©±ä»ÆµÄ¹ŲĻµĶ¼Ļó£¬ŌņaµÄÖµĪŖ£Ø””””£©

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
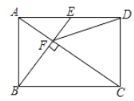
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬EŹĒAD±ßµÄÖŠµć£¬BE”ĶACÓŚµćF£¬Į¬½ÓDF£¬ĻĀĮŠĖÄøö½įĀŪ£ŗ¢Ł”÷AEF”×”÷CAB£»¢ŚCF£½2AF£»¢ŪDF£½DC£»¢ÜSĖıߊĪCDEF£½![]() S”÷ABF£®ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø £©øö
S”÷ABF£®ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø £©øö
A.4B.3C.2D.1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
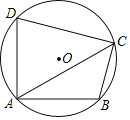
”¾ĢāÄæ”æŅŃÖŖĖıߊĪABCDÄŚ½ÓÓŚ”ŃO£¬”ĻDAB£½90”ć£®
£Ø¢ń£©ČōAB£½AD£¬Ēó”ĻACBµÄ¶ČŹż£»
£Ø¢ņ£©Į¬½ÓAC£¬ČōAD£½8£¬AB£½6£¬¶Ō½ĒĻßACĘ½·Ö”ĻDAB£¬ĒóACµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»“ĪŗÆŹż![]() Óė·“±ČĄżŗÆŹż
Óė·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóĻą½»ÓŚA£Ø©1£¬4£©£¬B£Ø2£¬n£©Į½µć£¬Ö±ĻßAB½»xÖįÓŚµćD£®
µÄĶ¼ĻóĻą½»ÓŚA£Ø©1£¬4£©£¬B£Ø2£¬n£©Į½µć£¬Ö±ĻßAB½»xÖįÓŚµćD£®
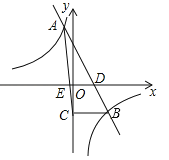
£Ø1£©ĒóŅ»“ĪŗÆŹżÓė·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©¹żµćB×÷BC”ĶyÖį£¬“¹×ćĪŖC£¬Į¬½ÓAC½»xÖįÓŚµćE£¬Ēó”÷AEDµÄĆ껿S£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży1£½k1x+2Óė·“±ČĄżŗÆŹży2£½![]() µÄĶ¼Ļó½»ÓŚµćA£Ø4£¬m£©ŗĶB£Ø©8£¬©2£©£¬ÓėyÖį½»ÓŚµćC£®
µÄĶ¼Ļó½»ÓŚµćA£Ø4£¬m£©ŗĶB£Ø©8£¬©2£©£¬ÓėyÖį½»ÓŚµćC£®
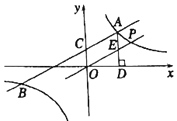
£Ø1£©k1£½”” ””£¬k2£½”” ””£»
£Ø2£©øł¾ŻŗÆŹżĶ¼ĻóæÉÖŖ£¬µ±y1£¾y2Ź±£¬xµÄȔֵ·¶Ī§ŹĒ”” ””£»
£Ø3£©¹żµćA×÷AD”ĶxÖįÓŚµćD£¬µćPŹĒ·“±ČĄżŗÆŹżŌŚµŚŅ»ĻóĻŽµÄĶ¼ĻóÉĻŅ»µć£®ÉčÖ±ĻßOPÓėĻ߶ĪAD½»ÓŚµćE£¬µ±SĖıߊĪODAC£ŗS”÷ODE£½3£ŗ1Ź±£¬ĒóÖ±ĻßOPµÄ½āĪöŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×ŪŗĻÓėĢ½¾æ
ČēĶ¼£¬Å×ĪļĻß![]() ¾¹żµćA(-2,0)£¬B(4,0)Į½µć£¬Óė
¾¹żµćA(-2,0)£¬B(4,0)Į½µć£¬Óė![]() Öį½»ÓŚµćC£¬µćDŹĒÅ×ĪļĻßÉĻŅ»øö¶Æµć£¬ÉčµćDµÄŗį×ų±źĪŖ
Öį½»ÓŚµćC£¬µćDŹĒÅ×ĪļĻßÉĻŅ»øö¶Æµć£¬ÉčµćDµÄŗį×ų±źĪŖ![]() .Į¬½ÓAC£¬BC£¬DB£¬DC£¬
.Į¬½ÓAC£¬BC£¬DB£¬DC£¬
(1)ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
(2)”÷BCDµÄĆ껿µČÓŚ”÷AOCµÄĆ껿µÄ![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄÖµ£»
掙术
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬ČōµćMŹĒ![]() ÖįÉĻµÄŅ»øö¶Æµć£¬µćNŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŹŌÅŠ¶ĻŹĒ·ń“ęŌŚÕāŃłµÄµćM,Ź¹µĆŅŌµćB£¬D£¬M£¬NĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
ÖįÉĻµÄŅ»øö¶Æµć£¬µćNŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŹŌÅŠ¶ĻŹĒ·ń“ęŌŚÕāŃłµÄµćM,Ź¹µĆŅŌµćB£¬D£¬M£¬NĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com