
 如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.
如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.
|


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
 甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.
甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.查看答案和解析>>
科目:初中数学 来源: 题型:
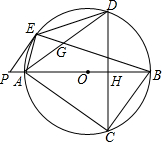 如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D. |
| BE |
查看答案和解析>>
科目:初中数学 来源: 题型:
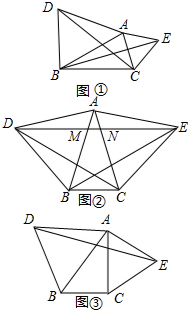 (1)如图①,在△ABC中,分别以AB,AC为边作等边△ABD和等边△ACE,猜想CD与BE有什么样的数量关系,直接写出结论,不需证明;
(1)如图①,在△ABC中,分别以AB,AC为边作等边△ABD和等边△ACE,猜想CD与BE有什么样的数量关系,直接写出结论,不需证明;查看答案和解析>>
科目:初中数学 来源: 题型:
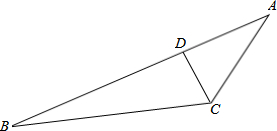 如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,则下列各式正确的是( )
如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,则下列各式正确的是( )| A、AD=BC-CA |
| B、AD=BC-CD |
| C、BD=AC+CD |
| D、AC=BD-AD |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
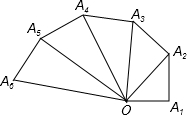 第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的.且OA1=A1A2=A2A3=A3A4=…=A9A10=1.如果把图中的直角三角形继续画下去,那么
第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的.且OA1=A1A2=A2A3=A3A4=…=A9A10=1.如果把图中的直角三角形继续画下去,那么查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com