
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E。

(1)求证:AB=BE;
(2)若PA=2 ,cosB=![]() ,求⊙O半径的长。
,求⊙O半径的长。
【答案】(1)、证明过程见解析;(2)、3.
【解析】
试题分析:(1)、连接OD,根据切线的性质得出∠PDA+∠ADO=90°,根据BE⊥PD得出∠E+∠EDC=90°,根据对顶角相等从而得出∠ADO=∠E,根据OA=OD得出∠OAD=∠ADO,从而说明∠OAD=∠E,从而得出答案;(2)、首先设半径为r,根据OD⊥PC,BE⊥PC得出OD∥BE,然后根据Rt△PDO中cos∠POD=cos∠B列出关于r的一元一次方程,求出r的值.
试题解析:(1)、连接OD, ∵PD切⊙O于点D,∴∠PDO=90°即∠PDA+∠ADO=90°,
∵BE垂直于PD,交PD的延长线于点C,∴∠E+∠EDC=90°, ∵∠PDA=∠EDC,∴∠ADO=∠E,
∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠E,∴AB=BE
(2)、设⊙O半径的半径为r ∵OD⊥PC,BE⊥PC,∴OD∥BE,∴∠POD=∠B,
∵在Rt△PDO中,PO=PA+AO=2+r,cos∠POD=cos∠B=![]()
∴![]() ,解得:r=3,答:⊙O半径的长为3
,解得:r=3,答:⊙O半径的长为3


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 对角线相等的四边形是矩形B. 对角线互相垂直的四边形是正方形
C. 平行四边形的对角线平分一组对角D. 矩形的对角线相等且互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
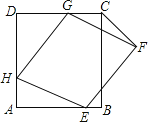
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初一所有学生将在大礼堂内参加2017年“元旦联欢晚会”,若每排坐30人,则有8人无座位;若每排坐31人,则空26个座位,则初一年级共有多少名学生?设大礼堂内共有x排座位,可列方程为______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=ax+2by﹣1(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a0+2b1﹣1=2b﹣1.
(1)已知T(1,﹣1)=﹣2,T(4,2)=3.
①求a,b的值;
②若关于m的不等式组 恰好有2个整数解,求实数p的取值范围;
恰好有2个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com