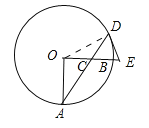
【题目】如图，OA，OB是⊙O的两条半径，OA⊥OB，C是半径OB上的一动点，连接AC并延长交⊙O于D，过点D作直线交OB延长线于E，且DE=CE，已知OA=8．
（1）求证：ED是⊙O的切线；
（2）当∠A=30°时，求CD的长．
【答案】（1）证明见解析；（2）
.
【解析】
（1）如图连接OD．欲证明DE是切线，只要证明OD⊥DE即可；
（2）解直角三角形求出OC，只要证明CD=OC即可解决问题；
（1）证明：如图连接OD．
∵OA=OD，∴∠A=∠ODA．
∵OA⊥OB，∴∠AOB=90°，∴∠A+∠ACO=90°．
∵ED=EB，∴∠EDB=∠EBD=∠ACO，∴∠ODA+∠EDC=90°，∴OD⊥DE，∴DE是⊙O的切线．
（2）在Rt△AOC中，∵OA=8，∠A=30°，∴OC=OAtan30°=．
∵OA=OD，∴∠ODA=∠A=30°，∠DOA=120°，∠DOC=30°，∴∠DOC=∠ODC=30°，∴CD=OC=．
阳光课堂同步练习系列答案科目：初中数学 来源： 题型：
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟．在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t
（分）之间的关系如图所示，下列结论：
①甲步行的速度为60米/分；
②乙走完全程用了30分钟；
③乙用16分钟追上甲；
④乙到达终点时，甲离终点还有320米
其中正确的结论有（ ）
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍，乒乓球每盒定价5元，乒乓球拍每副定价20元．现两家商店都搞促销活动，甲店每买一副球拍赠一盒乒乓球；乙店按九折优惠．某班级需购球拍4副，乒乓球x盒（x≥4）．
（1）若在甲店购买付款
（元），在乙店购买付款
（元），分别写出与x的函数关系式；
（2）买30盒乒乓球时，在哪家商店购买合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
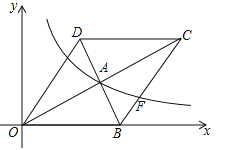
【题目】如图，在平面直角坐标系中，菱形OBCD的边OB在x轴上，反比例函数
（x＞0）的图象经过菱形对角线的交点A，且与边BC交于点F，点A的坐标为（4，2）．
（1）求反比例函数的表达式；
（2）求点F的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【提出问题】
（1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．
【类比探究】
（2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．
【拓展延伸】
（3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，
中，
、
两点分别是边
和
的垂直平分线与
的交点，连结
和
，且
.求
的度数.
证明：∵、两点分别是边和的垂直平分线与的交点，
∴
______________，
.( )
∵，
∴在
中，
___________________(等量代换)
∴是____________三角形.
∴
，
∵在
中，，
∴
____________.
又∵的外角，
∴
__________+∠___________
.
(三角形的一个外角等于与它不相邻的两个内角的和)
∴
____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BF⊥a于点F，DE⊥a于点E，若DE=8，BF=5，则EF的长为__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，使ΔABC≌ΔADC成立的条件是（ ）
A.AB=AD，∠B=∠DB.AB=AD，∠ACB=ACD
C.BC=DC，∠BAC=∠DACD.AB=AD，∠BAC=∠DAC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
