
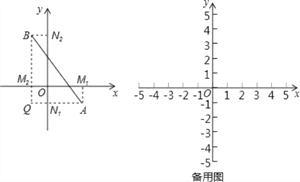
【题目】阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
(1)AB= .
(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为 ;
(3)根据阅读材料并利用平面内两点间的距离公式,求代数式![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)5;(3)
;(2)5;(3)
【解析】分析:(1)通过作铅垂线构造直角三角形,利用勾股定理进行求解即可,
(2)根据(1)结论代入两点坐标计算即可,(3) 代数式![]() +
+![]() 的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,可以通过作对称转化为两点间线段距离最短,再利用两点之间距离公式计算即可求解.
的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,可以通过作对称转化为两点间线段距离最短,再利用两点之间距离公式计算即可求解.
详解:(1)∵AB2=AQ2+BQ2=|x1﹣x2|2+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,
∴AB=![]() ,故答案为
,故答案为![]() .
.
(2)∵A(1,﹣3),B(﹣2,1),
∴AB=![]() =5,故答案为5.
=5,故答案为5.
(3)代数式![]() +
+![]() 的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,如图,
的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,如图,
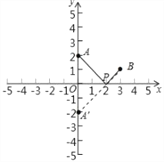
作A关于x轴的对称点A′,连接BA′与x轴的交点即为所求的点P.此时PA+PB最小,
∵A′(0,﹣2),B(3,1),
∴PA+PB=PA′+PB=BA′=![]() =3
=3![]()
∴代数式![]() +
+![]() 的最小值为3
的最小值为3![]() .
.


科目:初中数学 来源: 题型:
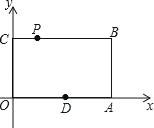
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的棱长为1cm的小正方体堆成一个几何体,如图所示:
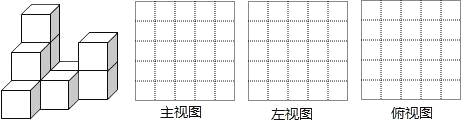
(1)这个几何体是由 个小正方体组成,请画出这个几何体的三视图;
(2)如果在这个几何体露在外面的表面喷上黄色的漆,每平方米用2克,则共需 克漆;
(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十 一”黄金周期间,我市庐山风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)、若9月30日的游客人数记为n,请用含n的代数式表示10月2日的游客________万人。
(2)、请判断七天内游客人数最多的是_______日;最少的是______日;它们相差_____万人。
(3)、以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数变化情况:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用“”表示一种新运算符号,观察下列式子,解决问题:
25=2×2+4=8
34=2×3+3=9
3(﹣1)=2×3﹣2=4
﹣3(﹣5)=2×(﹣3)﹣6=﹣12
……
(1)请你用含a,b的式子表示这个规律:求ab的值;
(2)求(﹣![]() 6)(﹣4)的值;
6)(﹣4)的值;
(3)如果x(﹣3)=3x,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张用 6000 元购进 A,B 两种服装,按标价售出后可获得毛利 3800元(毛利=售价﹣进价).现已知 A 种服装的进价是 60 元/件,标价是 100 元/件;B 种服装的进价是 100 元/件,标价是 160 元/件.
(1)这两种服装各购进了多少件?
(2)如果 A 种服装按标价的 8 折出售,B 种服装按标价的 7 折出售,那么这批服装全部售完后,小张比按标价出售少收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com