
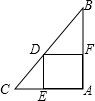
 如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$.
如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$. 分析 证明△BDF∽△ACB,列出比例式即可解决问题.
解答 解:∵四边形DEAF是正方形,
∴DF∥AC,DF=DE=AE,∠AFD=∠DEA=90°,
∴$\frac{BF}{BA}$=$\frac{DF}{AC}$,
设正方形的边长为x,则BF=16-x,
∴$\frac{16-x}{16}$=$\frac{x}{8}$,
∴x=$\frac{16}{3}$,
∴正方形的边长为$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 该题主要考查了相似三角形的判定及其性质、正方形的性质等几何知识点的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合运用能力提出了一定的要求.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
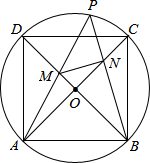 如图,正方形ABCD内接于⊙O,P为劣弧$\widehat{CD}$上一点,PA交BD于点M,PB交AC于点N,记∠PBD=θ.若MN⊥PB,则2cos2θ-tanθ的值( )
如图,正方形ABCD内接于⊙O,P为劣弧$\widehat{CD}$上一点,PA交BD于点M,PB交AC于点N,记∠PBD=θ.若MN⊥PB,则2cos2θ-tanθ的值( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
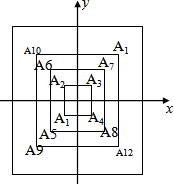 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 A1,A2,A3,A4,…表示,则顶点A2013的坐标是(-504,-504).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 A1,A2,A3,A4,…表示,则顶点A2013的坐标是(-504,-504).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
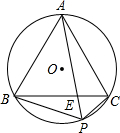 如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
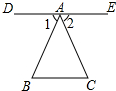 如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.
如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1.5,b=2,c=3 | B. | a=7,b=24,c=25 | C. | a=6,b=8,c=10 | D. | a=5,b=12,c=13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com