
| A. | $\frac{4}{5}$cm | B. | $\sqrt{5}$cm | C. | 2cm | D. | $2\sqrt{5}$cm |
分析 设圆锥的母线长为lcm,根据圆锥的侧面积为侧面展开图中扇形的面积得出$\frac{144π×{l}^{2}}{360}$=10π,求出l=5,再设圆锥的底面半径是rcm,根据圆锥的底面圆周长是扇形的弧长得出2πr=$\frac{144π×5}{180}$,解方程即可求出半径.
解答 解:设圆锥的母线长为lcm,则$\frac{144π×{l}^{2}}{360}$=10π,
解得:l=5,
设圆锥的底面半径是rcm,则2πr=$\frac{144π×5}{180}$,
解得:r=2.
即这个圆锥的底面半径为2cm,
故选C.
点评 本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{8}{5}$ | B. | 8 | C. | -8 | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
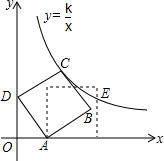 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,点A的坐标为(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是1+$\frac{\sqrt{3}}{3}$.
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,点A的坐标为(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是1+$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com