
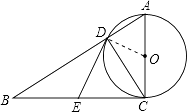
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2 ![]() ,则DE=;
,则DE=;
②当∠B=°时,以O,D,E,C为顶点的四边形是正方形.
【答案】
(1)
证明:连接OD.
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵E为BC边的中点,
∴DE为直角△DCB斜边的中线,
∴DE=CE= ![]() .
.
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)3;45
【解析】(2)解:①∵∠B=30°,AC=2 ![]() ,∠BCA=90°,
,∠BCA=90°,
∴tan30°= ![]() =
= ![]() =
= ![]() ,
,
解得:BC=6,
则DE= ![]() BC=3;
BC=3;
故答案为:3;
②当∠B=45°时,四边形ODEC是正方形,
∵∠ACB=90°,
∴∠A=45°,
∵OA=OD,
∴∠ADO=45°,
∴∠AOD=90°,
∴∠DOC=90°,
∵∠ODE=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴矩形DECO是正方形.
故答案为:45.
(1)运用垂径定理、直角三角形的性质证明∠ODE=90°即可解决问题;(2)①直接利用锐角三角函数关系得出BC的长,再利用直角三角形的性质得出DE的长;②当∠B=45°时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.


科目:初中数学 来源: 题型:
【题目】在所给图形中:
⑴求证:∠BDC=∠A+∠B+∠C;
⑵如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠B、∠C这4个角之间有怎样的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各题:
+3 +2 +1 0 -2
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最小,最小值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1-(-2)]),请另写出两种符合要求的运算式子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 的表达式为
的表达式为![]() ,点A,B的坐标分别为
,点A,B的坐标分别为
(1,0),(0,2),直线AB与直线![]() 相交于点P.
相交于点P.
(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线![]() 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为 . 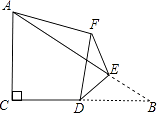
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,![]() ∠BOD=∠DOE.
∠BOD=∠DOE.
(1)求∠BOF的度数;
(2)请写出图中与∠BOD相等的所有的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提升企业产品竞争力,某企业加大了科研经费的投入,2016年该企业投入科研经费5000万元,2018年投入科研经费7200万元,假设该企业这两年投入科研经费的年平均增长率相同.
![]() 求这两年该企业投入科研经费的年平均增长率.
求这两年该企业投入科研经费的年平均增长率.
![]() 若该企业科研经费的投入还将保持相同的年平均增长率,请你预算2020年该企业投入科研经费多少万元.
若该企业科研经费的投入还将保持相同的年平均增长率,请你预算2020年该企业投入科研经费多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某工厂货物传送带的平面示意图,为提高传送过程的安全性,工厂计划改造传动带与地面的夹角,使其AB的坡角由原来的43°改为30°.已知原传送带AB长为5米.求新旧货物传送带着地点B、C之间相距多远?(结果保留整数,参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,点E、F分别在边AB、AC上,将
,点E、F分别在边AB、AC上,将![]() 沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且
沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且![]() .
.
![]() 求证:四边形AFDE是菱形.
求证:四边形AFDE是菱形.
![]() 若
若![]() ,
,![]() ,求线段ED的长度.
,求线段ED的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com